Back to Subject

Practice MCQ Subjective

Unit 2 - Notes

PEA305

Unit 2: Percentage, Profit Loss Discount

Part 1: Fundamentals of Percentage

1. Concept and Calculation

Percentage comes from the Latin "per centum," meaning "by the hundred." It is a fraction with a denominator of 100.

Symbol: $\%$
Meaning: $x\% = \frac{x}{100}$

Basic Calculation:
To find $y\%$ of $x$ :

\text{Value} = x \times \frac{y}{100}

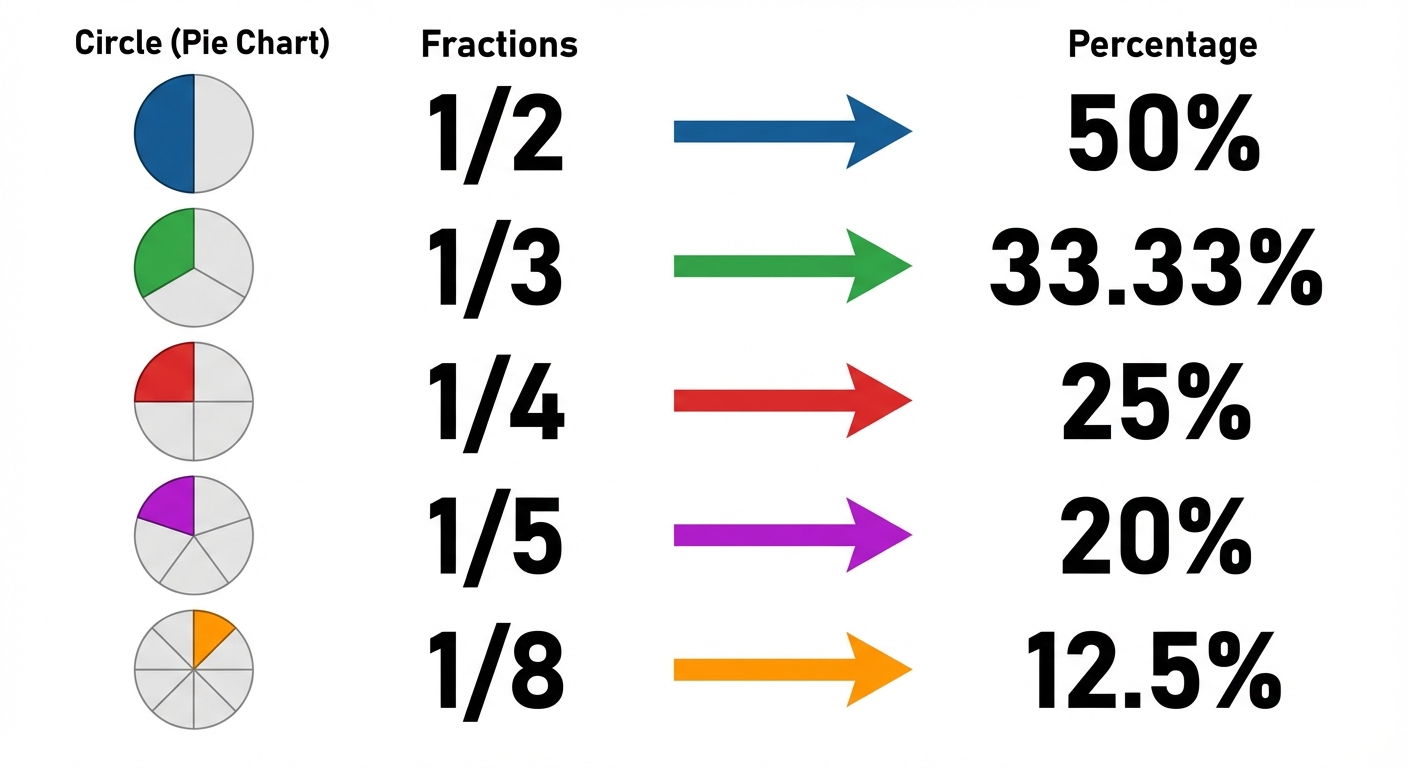
2. Percentage to Fraction Conversion

Speed in calculation relies heavily on memorizing standard percentage-to-fraction equivalents. This eliminates the need to divide by 100 manually during complex problems.

Fraction	Percentage	Decimal	Fraction	Percentage	Decimal
$1/1$	$100\%$	$1.0$	$1/7$	$14.28\%$	$0.1428$
$1/2$	$50\%$	$0.5$	$1/8$	$12.5\%$	$0.125$
$1/3$	$33.33\%$	$0.33$	$1/9$	$11.11\%$	$0.111$
$1/4$	$25\%$	$0.25$	$1/10$	$10\%$	$0.1$
$1/5$	$20\%$	$0.2$	$1/11$	$9.09\%$	$0.0909$
$1/6$	$16.66\%$	$0.166$	$1/12$	$8.33\%$	$0.0833$

A detailed reference chart and visualization showing the conversion between circles (pie charts), fr... — AI-generated image — may contain inaccuracies

3. Percentage Comparison

This involves comparing two values, $A$ and $B$ .

A is what % of B? $\rightarrow \frac{A}{B} \times 100$
A is what % more than B? $\rightarrow \frac{A - B}{B} \times 100$
A is what % less than B? $\rightarrow \frac{B - A}{B} \times 100$

Key Rule: The value mentioned after "than" or "of" is usually the base (denominator).

4. Successive Percentage Change

If a value changes by $x\%$ and then by $y\%$ , the net percentage change is not simply $x+y$ .

Formula Method:

\text{Net Change} \% = x + y + \frac{xy}{100}

Use positive signs for increase and negative signs for decrease.

Multiplication Factor Method:
If a number increases by $20\%$ and then decreases by $10\%$ :

\text{Final Value} = \text{Initial Value} \times 1.2 \times 0.9

Part 2: Applications of Percentage

1. Problems Based on Marks

Usually involves a student scoring $x\%$ marks and failing by $A$ marks, while another scores $y\%$ marks and gets $B$ marks more than the passing score.

Concept: The difference in percentage corresponds to the difference in absolute marks.
$(y - x)\% \text{ of Total Marks} = A + B$

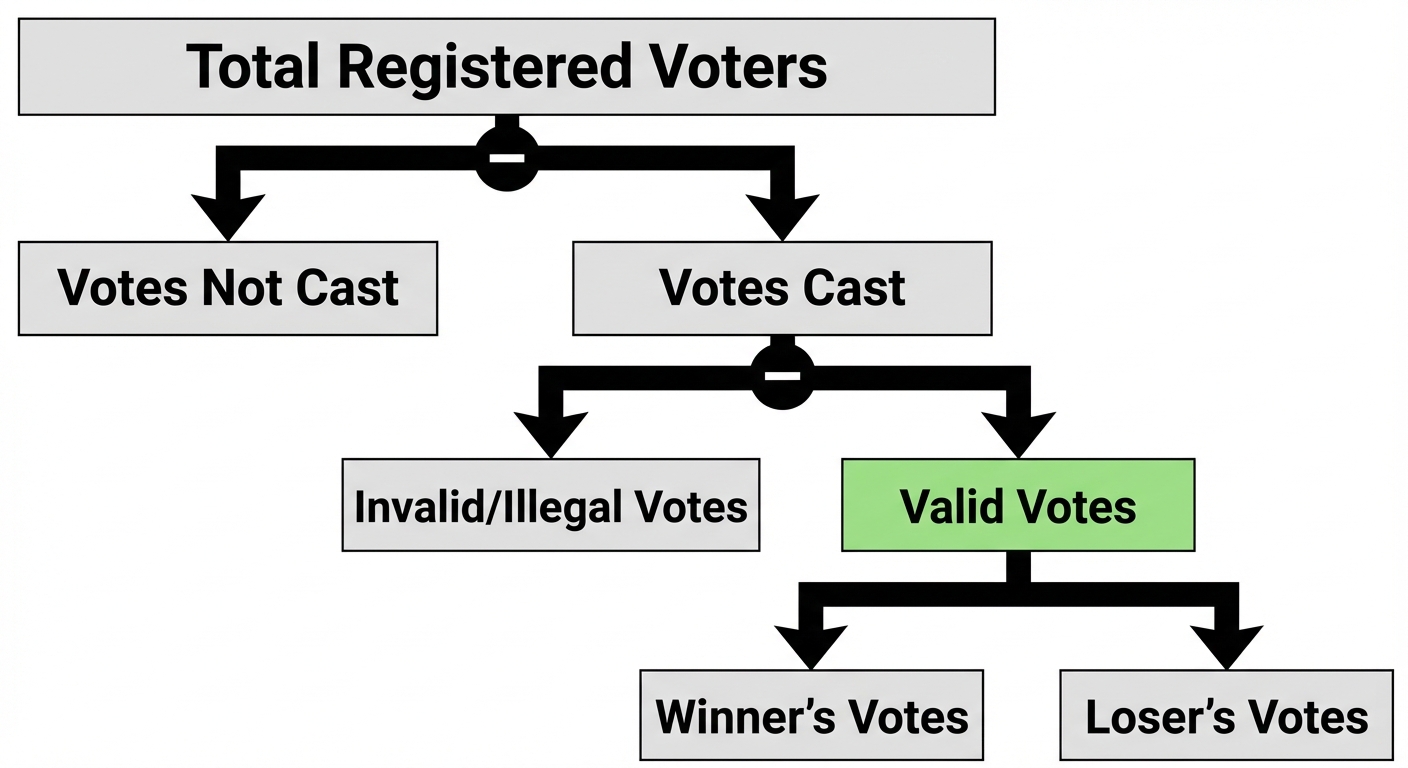
2. Problems Based on Elections

These problems typically involve a hierarchy of votes.

Total Voters: Everyone on the list.
Votes Cast: Total Voters minus those who didn't vote.
Valid Votes: Votes Cast minus Invalid/Illegal votes.
Winner's Votes: Usually a percentage of Valid Votes (read question carefully).

A vertical flowchart diagram illustrating the logic of Election Problems. The top box is "Total Regi... — AI-generated image — may contain inaccuracies

3. Population and Depreciation

These follow the concept of Compound Interest.
If current population is $P$ and rate of growth is $R\%$ :

Population after n years: $P \times (1 + \frac{R}{100})^n$
Population n years ago: $\frac{P}{(1 + \frac{R}{100})^n}$

For depreciation (value of machine decreasing), use a minus sign inside the bracket: $(1 - \frac{R}{100})$ .

4. Percentage Error

This measures the inaccuracy in a measurement relative to the true value.

\text{Percentage Error} = \frac{\text{Error}}{\text{True Value}} \times 100

Error = |True Value - Measured Value|

Part 3: Profit, Loss, and Discount

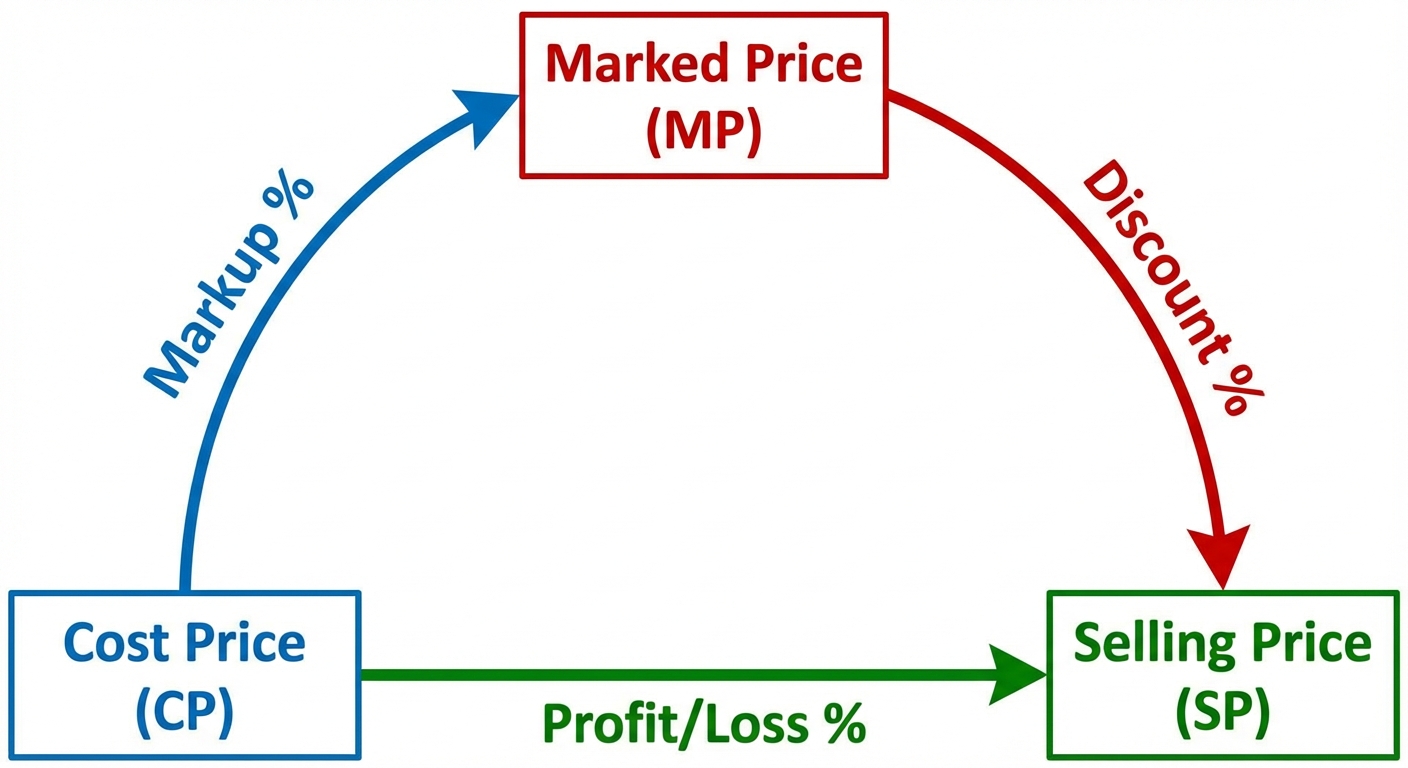
1. Fundamental Terminologies

Cost Price (CP): The price at which an article is purchased. This includes overheads (transport, repair).
Selling Price (SP): The price at which the article is sold.
Marked Price (MP): The price printed on the label (List Price/Tag Price).

2. Profit and Loss Calculations

Profit and Loss are always calculated on the Cost Price unless specified otherwise.

Profit: $SP > CP \rightarrow \text{Profit} = SP - CP$
Loss: $CP > SP \rightarrow \text{Loss} = CP - SP$
Profit %: $\frac{\text{Profit}}{CP} \times 100$
Loss %: $\frac{\text{Loss}}{CP} \times 100$

Calculating SP from CP:

$SP = CP \times \frac{100 + P\%}{100}$ (in case of Profit)
$SP = CP \times \frac{100 - L\%}{100}$ (in case of Loss)

3. Discount and Marked Price

Discount is always calculated on the Marked Price (MP).

Discount: $MP - SP$
Discount %: $\frac{\text{Discount}}{MP} \times 100$
Selling Price (related to MP): $SP = MP \times \frac{100 - D\%}{100}$

A triangular conceptual diagram showing the cyclical relationship between Cost Price (CP), Marked Pr... — AI-generated image — may contain inaccuracies

4. Relation between CP and MP

When a trader allows a discount of $D\%$ and still gains a profit of $P\%$ :

\frac{CP}{MP} = \frac{100 - \text{Discount} \%}{100 + \text{Profit} \%}

This formula is a shortcut to avoid calculating SP intermediately.

Part 4: Advanced Profit/Loss Scenarios

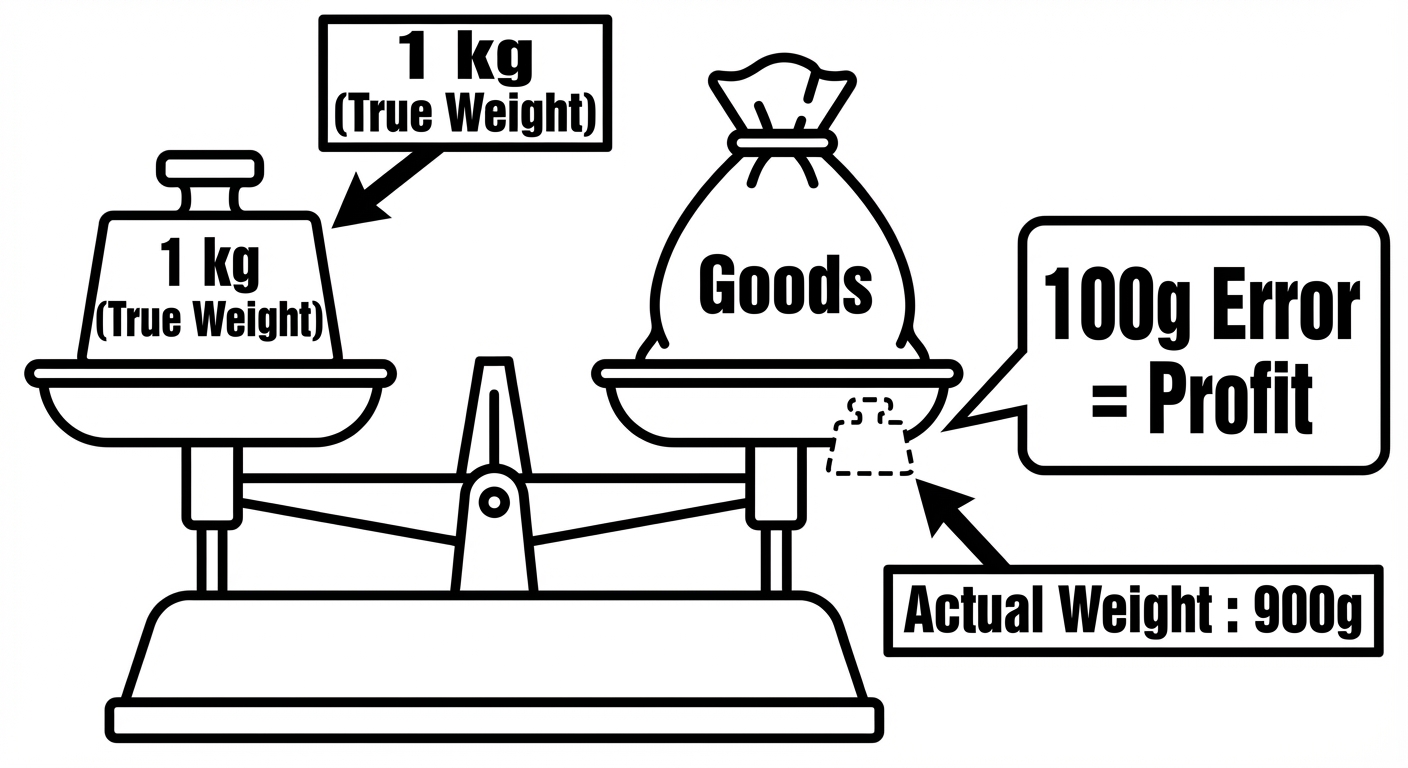
1. Dishonest Dealer (Faulty Weights)

A dealer claims to sell at Cost Price but uses a false weight (e.g., uses a 900g weight instead of 1kg).

Concept: The dealer saves goods, which equates to profit.
Formula:
- Example: If using 900g instead of 1000g: Error is 100g.
- $\text{Gain } \% = \frac{100}{1000 - 100} \times 100 = \frac{100}{900} \times 100 = 11.11\%$

A schematic diagram illustrating the "Dishonest Dealer" concept using an old-fashioned balance scale... — AI-generated image — may contain inaccuracies

2. Problems Based on Number of Articles

Sometimes CP and SP are given in terms of quantity rather than currency.

Example: CP of 15 articles equals SP of 12 articles.
Method: Assume the price of 1 article = 1 unit or take the LCM of the quantities.
Shortcut Formula:
- (Note: The denominator is Articles Sold, not Bought).

3. Common Selling Price (Same SP)

If two articles are sold at the same Selling Price, where one is sold at $x\%$ profit and the other at $x\%$ loss:

Result: There is ALWAYS a net LOSS.
Loss Formula:
$\text{Net Loss } \% = (\frac{x}{10})^2$
Note: This formula only applies when the Selling Price is the same and the numerical value of profit % and loss % is the same.