Unit 5: Permutation and combination, Probability

1. Principles of Counting

Before diving into formulas, it is crucial to understand the two fundamental principles that govern counting techniques.

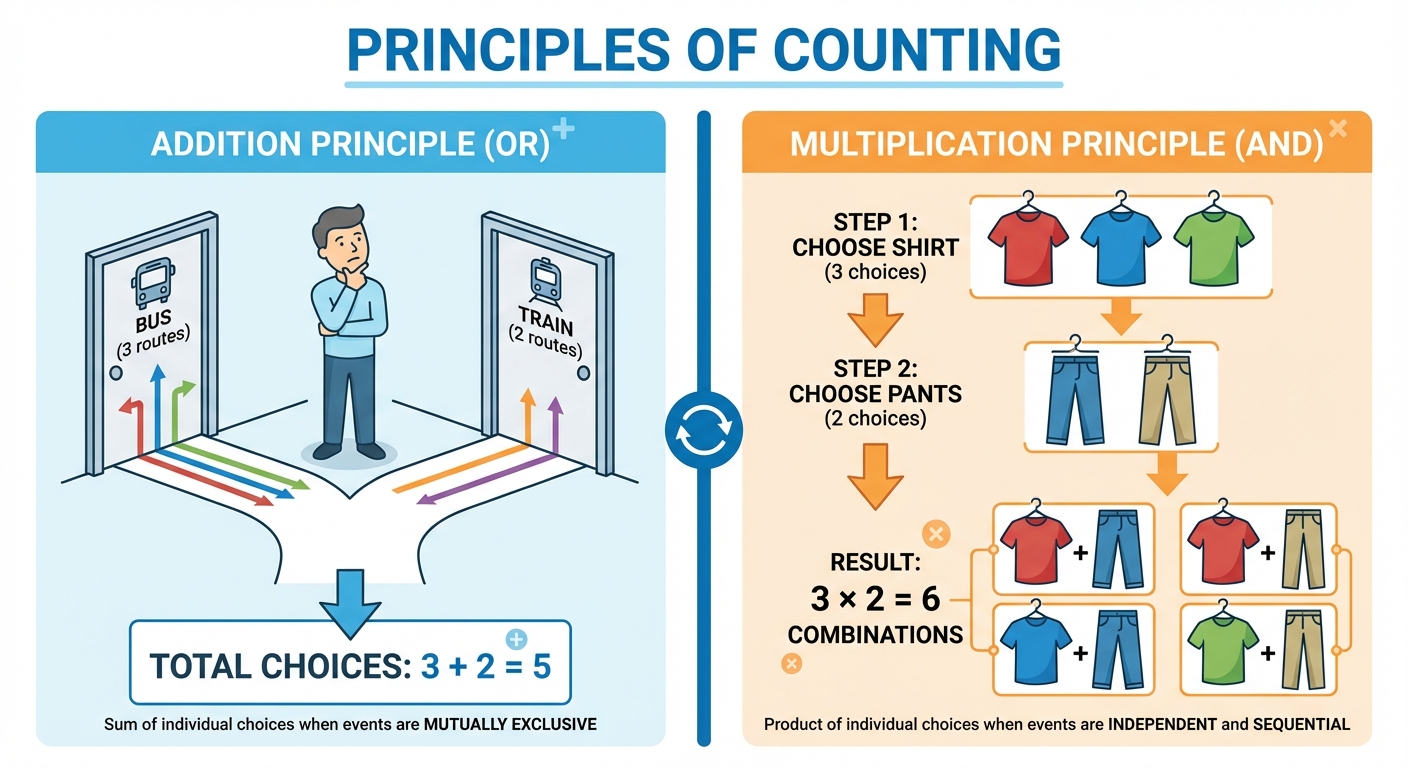
The Fundamental Principle of Addition (OR Rule)

If there are ways to perform task A and ways to perform task B, and the tasks are mutually exclusive (they cannot happen at the same time), then there are ways to perform either task A or task B.

• Keyword: "OR"
• Example: You have 3 shirts and 4 t-shirts. You want to wear one top. You can choose in ways.

The Fundamental Principle of Multiplication (AND Rule)

If a procedure involves a sequence of two independent tasks, where the first task can be done in ways and the second task can be done in ways, then the total number of ways to perform the procedure (Task A and Task B) is .

• Keyword: "AND" / "THEN"
• Example: You have 3 shirts and 2 pairs of pants. An outfit consists of one shirt and one pair of pants. Total outfits = ways.

2. Permutation (Arrangement)

Permutation refers to the arrangement of objects in a definite order. The order of elements matters.

Formula

The number of permutations of different objects taken at a time is denoted by :

Where . Note that .

Problems Based on Numbers

• Repetition Allowed: If places are to be filled by items and repetition is allowed, the number of ways is .
• Zero Constraints: When forming numbers (e.g., 3-digit numbers) using digits including 0, the first position cannot be 0.
• Divisibility:
  • Even numbers: Unit digit must be 0, 2, 4, 6, 8.
  • Divisible by 4: Last two digits must form a number divisible by 4.
  • Divisible by 5: Unit digit must be 0 or 5.

Problems Based on Words

• Unique Letters: If a word has distinct letters, they can be arranged in ways.
• Repetitive Letters: If there are objects of which are alike of one kind, are alike of second kind, and remaining distinct, the number of permutations is:
  
  • Example: ARRANGEMENT. Total = 11. A=2, R=2, N=2, E=2. Ways = .

Rank of a Word (Dictionary Order)

To find the rank of a word, arrange all permutations of its letters alphabetically.
Algorithm:

1. Alphabetize the letters of the given word.
2. Fix the first letter in alphabetical order and count permutations of remaining letters.
3. If the fixed letter matches the target word's first letter, freeze it and move to the second letter.
4. Sum the totals and add 1 for the word itself.

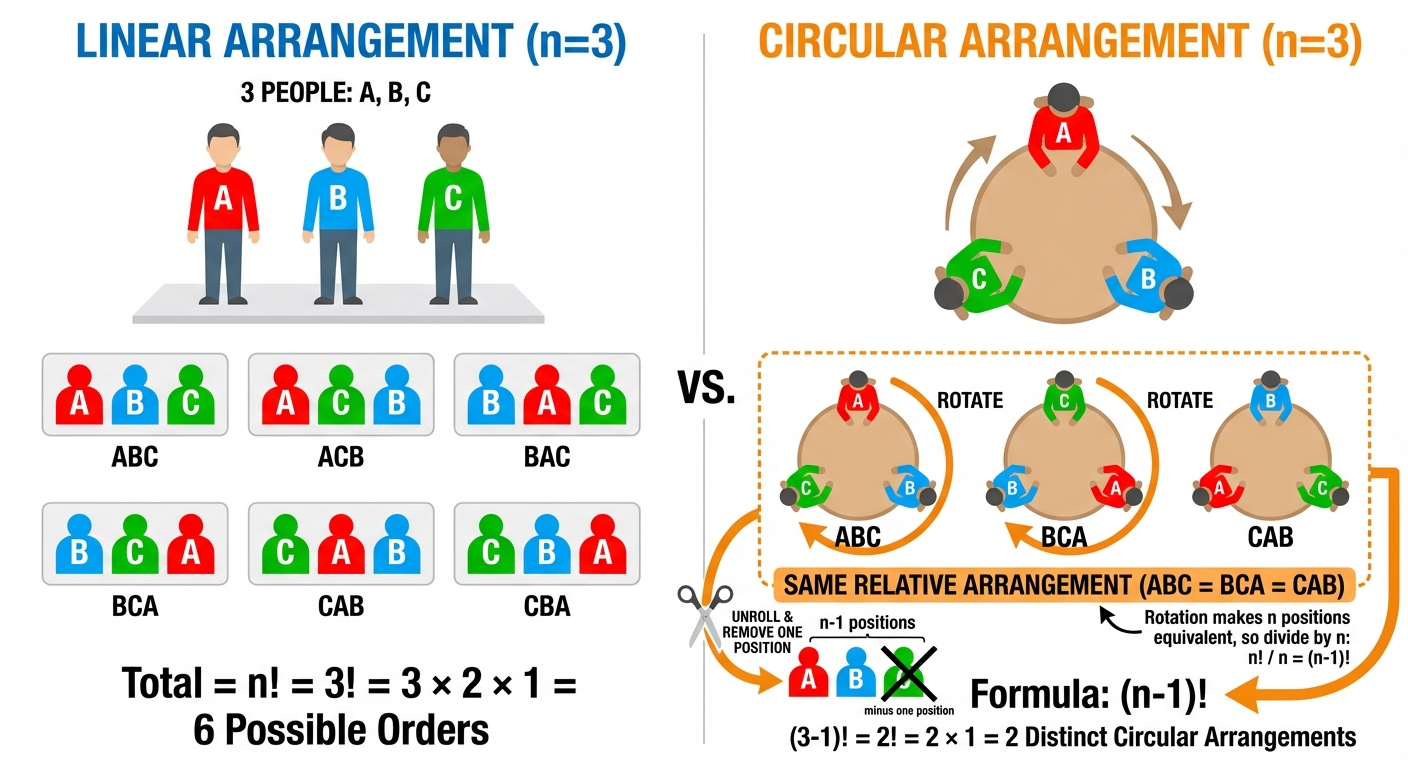
Circular Arrangement

• Distinct Objects: Arrangements of distinct objects around a circular table = . This is because relative order matters, not absolute position.
• Necklaces/Garlands: If clockwise and anti-clockwise arrangements are considered identical (e.g., beads on a necklace), the number of arrangements = .

3. Combination (Selection)

Combination refers to the selection of objects where order does not matter. AB and BA are treated as the same group.

Formula

The number of combinations of different objects taken at a time is denoted by :

Key Relationship: (Arrangement = Selection Ordering).

Important Properties

2. and
3. Pascal's Identity:

Distribution Problems

• Distinct Groups: Dividing distinct items into groups of size (where ):
  
• Identical Groups: If the groups are of equal size () and unordered, divide by the factorial of the number of groups ():
  

Geometric Applications

1. Straight Lines: From points where no 3 are collinear: .
   • Exception: If points are collinear: .
2. Triangles: From points: .
   • Exception: If points are collinear: .
3. Diagonals in a Polygon: Number of diagonals in an -sided polygon:
   

4. Concept of Probability

Probability is the measure of the likelihood that an event will occur.

Terminology

• Random Experiment: An experiment where outcomes cannot be predicted with certainty (e.g., tossing a coin).
• Sample Space (): The set of all possible outcomes.
• Event (): A subset of the sample space.

Mathematical Definition

5. Classification of Events

1. Simple vs. Compound: Simple events correspond to a single outcome. Compound events involve multiple outcomes.
2. Mutually Exclusive (Disjoint): Two events A and B cannot occur simultaneously.
3. Exhaustive Events: A set of events whose union equals the sample space. At least one must occur.
4. Independent Events: The occurrence of one event does not affect the probability of the other.
5. Complementary Event: The event that A does not occur ( or ).

6. Problems Based on Coins, Dice, and Cards

Coins

• Sample space for 1 coin: ()
• Sample space for coins: Total outcomes = .
• Example (3 coins): {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}.

Dice

• Sample space for 1 die: ()
• Sample space for dice: Total outcomes = .
• Common Problem: Sum of numbers on two dice. (Min sum 2, Max sum 12).

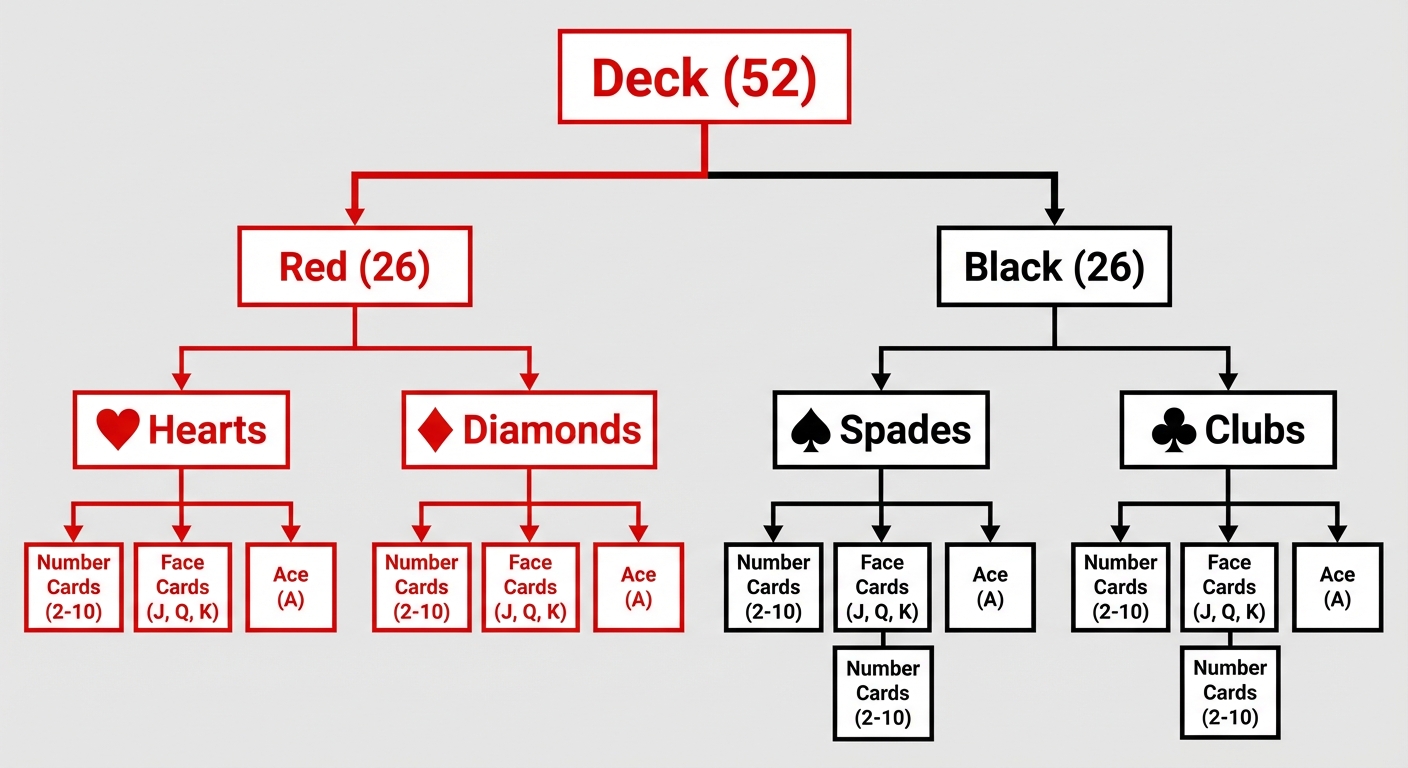
Playing Cards (Standard Deck of 52)

It is vital to memorize the structure of a deck of cards for probability problems.

• Total: 52 Cards.
• Colors: Red (26), Black (26).
• Suits: Hearts (Red), Diamonds (Red), Spades (Black), Clubs (Black) — 13 cards each.
• Ranks: 2, 3, 4, 5, 6, 7, 8, 9, 10, J, Q, K, A.
• Face Cards: Jack, Queen, King (Total 12: 3 per suit).
• Honor Cards: A, K, Q, J (Total 16).

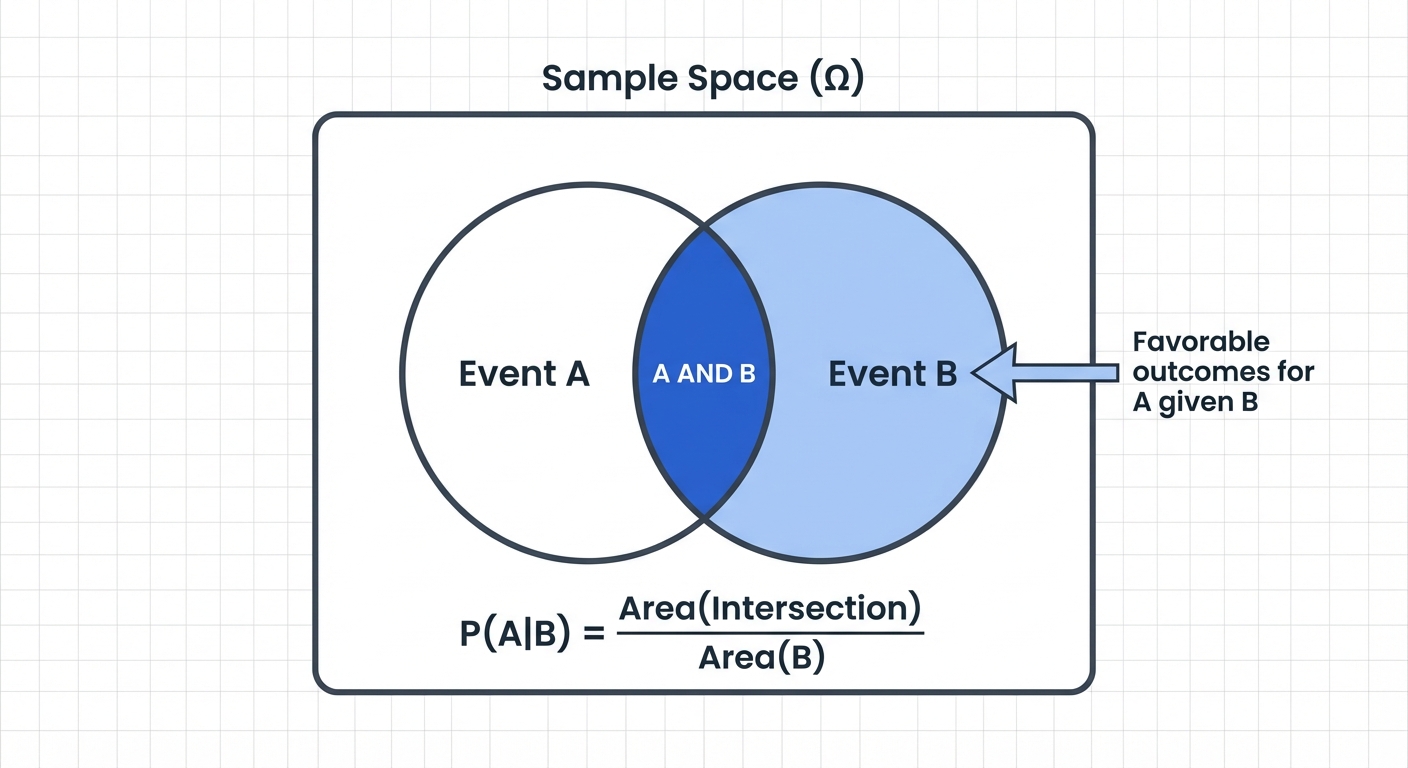
7. Conditional Probability

Conditional Probability is the probability of an event A occurring given that another event B has already occurred.

Formula

• : Probability of A given B.
• : Probability of both A and B happening.
• : Probability of the condition B.

Multiplication Theorem

Derived from the definition of conditional probability:

Bayes' Theorem (Brief Overview)

Used to find reverse probability. If are mutually exclusive and exhaustive events, and is any event associated with them: