Unit 4: Ratio and proportions, Alligation and mixtures

1. Concept of Ratio and Proportion

1.1 Ratio

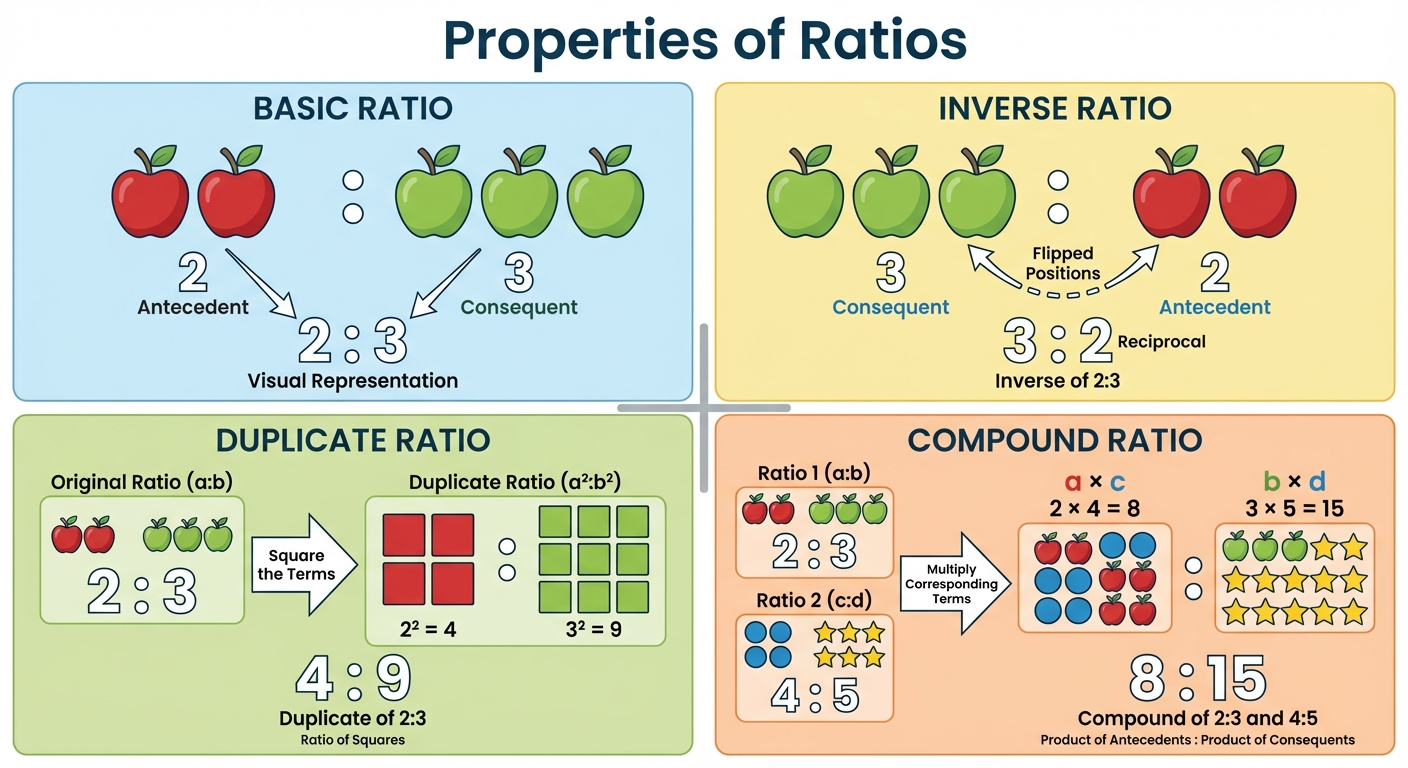
A Ratio is a comparison of two quantities of the same kind and in the same units. It is obtained by dividing the first quantity by the second.

• Notation: The ratio of to is written as or .
• Terms: In the ratio , is called the antecedent and is called the consequent.

Key Properties:

1. Multiplication/Division: A ratio remains unaltered if its numerator and denominator are multiplied or divided by the same non-zero number.
2. Inverse Ratio: The inverse ratio of is (or ).
3. Compound Ratio: The compound ratio of , , and is .
4. Duplicate Ratio: The duplicate ratio of is .
5. Sub-duplicate Ratio: The sub-duplicate ratio of is .

1.2 Proportion

Proportion is the equality of two ratios. If , then are said to be in proportion.

• Notation:
• Terms: and are called Extremes; and are called Means.

Fundamental Rule of Proportion:

Types of Proportions:

1. Fourth Proportional: If , then is the fourth proportional. ()
2. Third Proportional: If , then is the third proportional to and . ()
3. Mean Proportional: The mean proportional between and is .

2. Problems Based on Ages and Partnership

2.1 Problems on Ages

These problems deal with finding the age of an individual or the ratio of ages at different points in time (Past, Present, Future).

Core Methodology:

1. Assume the present age of the person to be (or multiple variables for two people).
2. "t years ago": The age was .
3. "t years hence" (later): The age will be .
4. If the current ratio of ages is , assume ages are and .

Common Problem Type:

• Statement: "Ten years ago, A was half of B in age. If the ratio of their present ages is 3:4, what will be the total of their present ages?"
• Solution Approach: Set present ages as and . Formulate equation: . Solve for .

2.2 Partnership

Partnership deals with business relationships where two or more people invest money to run a business and share profits/losses.

Fundamental Principle:

Where is the Investment amount and is the Time period of investment.

Types of Partnership:

1. Simple Partnership: All partners invest for the same time period. Profit is distributed in the ratio of investments ().
2. Compound Partnership: Partners invest different amounts for different time periods. Profit is distributed in the ratio of the product of investment and time ().

Working Partner vs. Sleeping Partner:

• Working Partner: Manages the business and often receives a salary or fixed percentage of profit before the remaining profit is divided based on investment.
• Sleeping Partner: Invests money but does not manage; only receives a share of profit based on investment.

3. Alligation and Mixtures

3.1 Concept of Mixture

A mixture is created by mixing two or more ingredients together. The value (price or concentration) of the mixture is called the Mean Price or Mean Value.

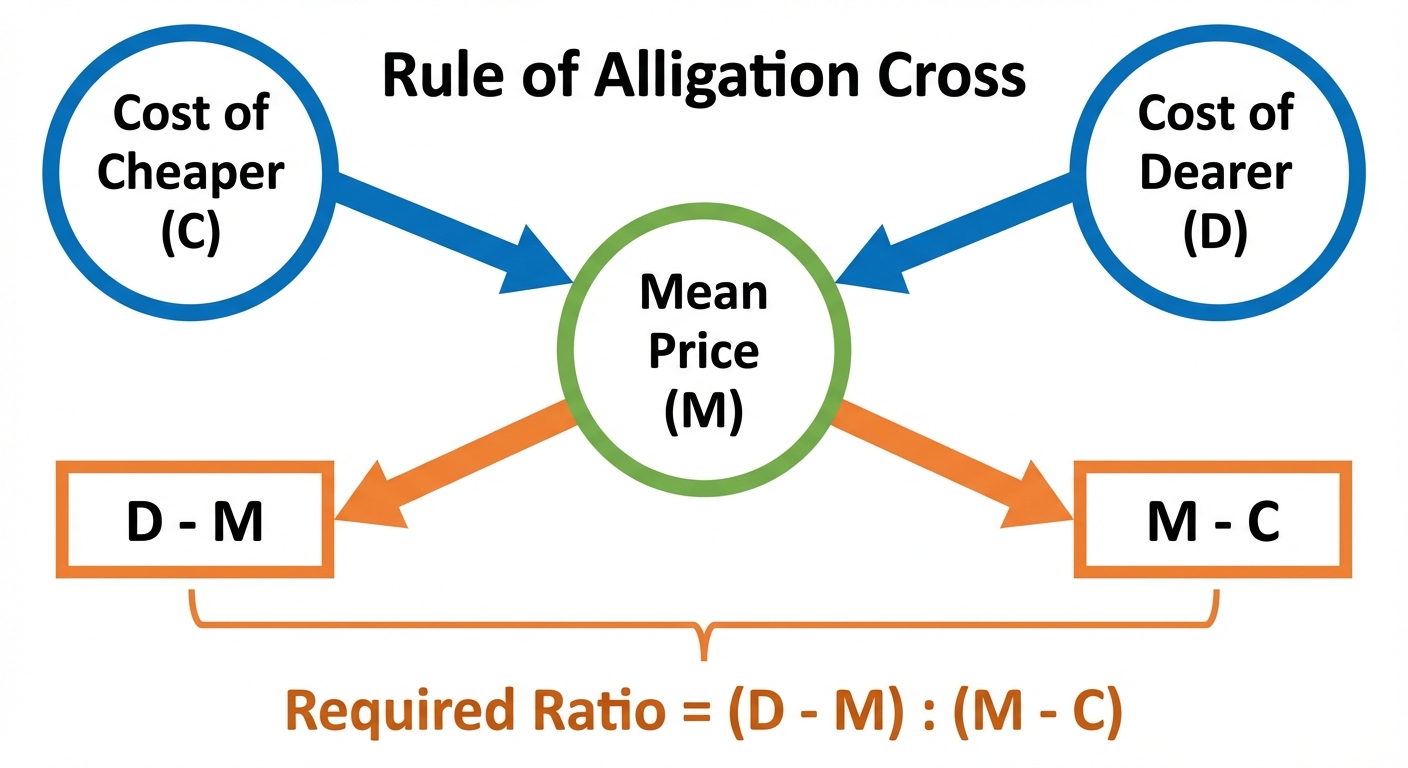
3.2 Rule of Alligation (The Cross Method)

Alligation is a rule that enables us to find the ratio in which two or more ingredients at given prices must be mixed to produce a mixture of a desired price.

Variables:

• : Cost of the Cheaper ingredient (unit price).
• : Cost of the Dearer (more expensive) ingredient (unit price).
• : Mean price of the mixture (unit price).

Constraint:

The Rule:

Visual Representation (The Cross):

      Cheaper Price (C)           Dearer Price (D)
             \                         /
              \                       /
               \                     /
                \                   /
                 \                 /
                  \               /
                    Mean Price (M)
                  /               \
                 /                 \
                /                   \
               /                     \
              /                       \
             /                         \
    (D - M)                           (M - C)
[Ratio of Cheaper]                 [Ratio of Dearer]

3.3 Important Notes on Alligation

1. Same Units: All values (, , and ) must be in the same unit (e.g., all Cost Prices). You cannot mix Cost Price with Selling Price directly.
2. Water in Milk: In problems involving mixing water with milk to gain profit, the cost of water is usually taken as 0, unless specified otherwise.
3. Speed and Time: If Alligation is applied to Speed (), the resulting ratio is the ratio of Time, not distance.

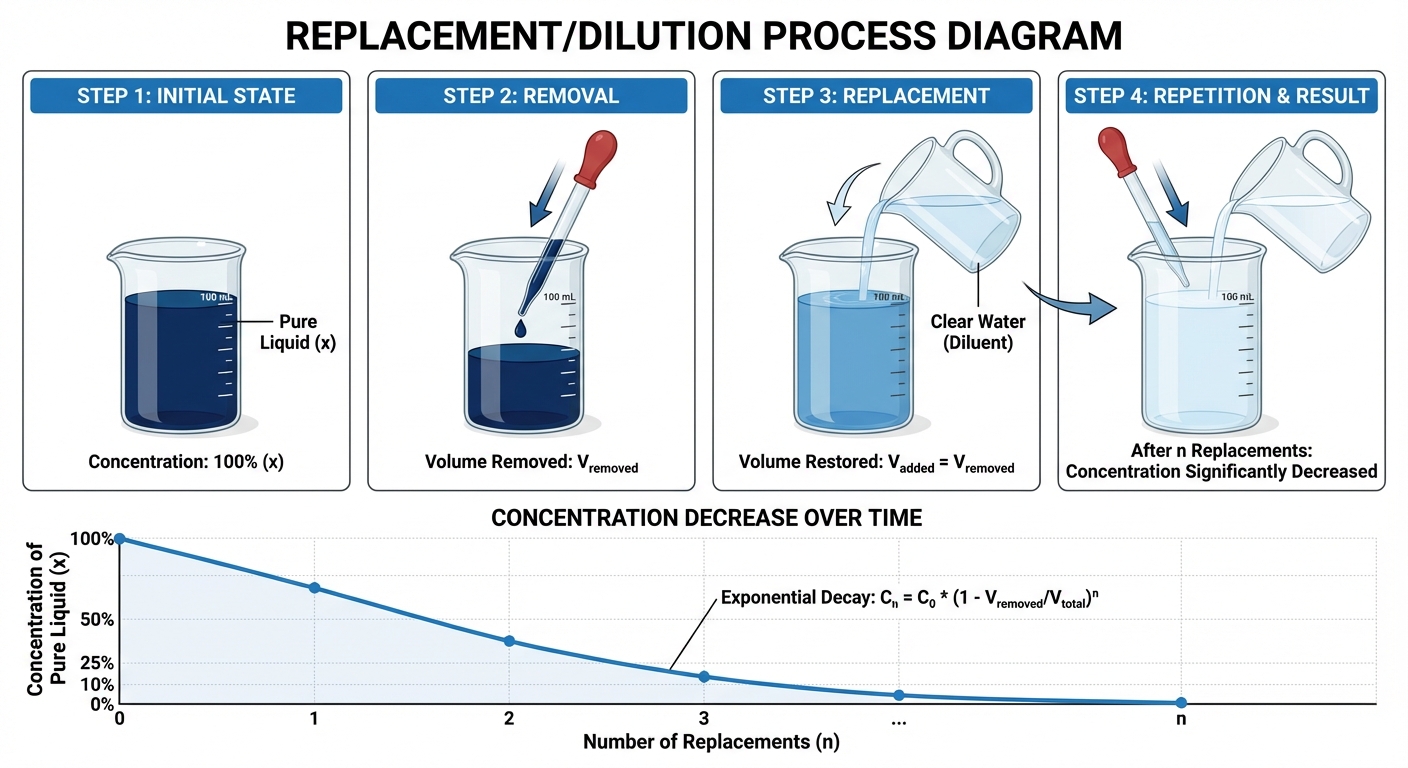
4. Replacement Based Questions

These questions involve the repeated removal of a specific quantity of liquid from a vessel and replacing it with another liquid (usually water).

4.1 Concept

When a part of a solution is removed and replaced with a solvent (like water), the concentration of the solute (pure liquid) decreases in a geometric progression.

4.2 The General Formula

If a vessel initially contains units of a pure liquid, and units are taken out and replaced by water, and this operation is repeated times, then:

Where:

• = Initial quantity of pure liquid.
• = Quantity removed and replaced in each step.
• = Number of times the process is performed.

4.3 Step-by-Step Logic (Without Formula)

For complex problems (e.g., different amounts removed each time), use the fractional multiplier method:

1. Step 1: Calculate the fraction of liquid remaining after one operation.
   • Fraction remaining =
2. Step 2: If the operation is repeated, multiply the fractions.

Example:

• Problem: From 100L of pure milk, 10L is replaced by water. This is done twice.
• Solution:
  • Total = 100L. Removed = 10L.
  • Remaining Milk Factor = (or 90%).
  • After 2 steps: Liters of milk.