Unit 5: Graphs theory II

1. Planar Graphs and Euler’s Formula

Planar Graphs

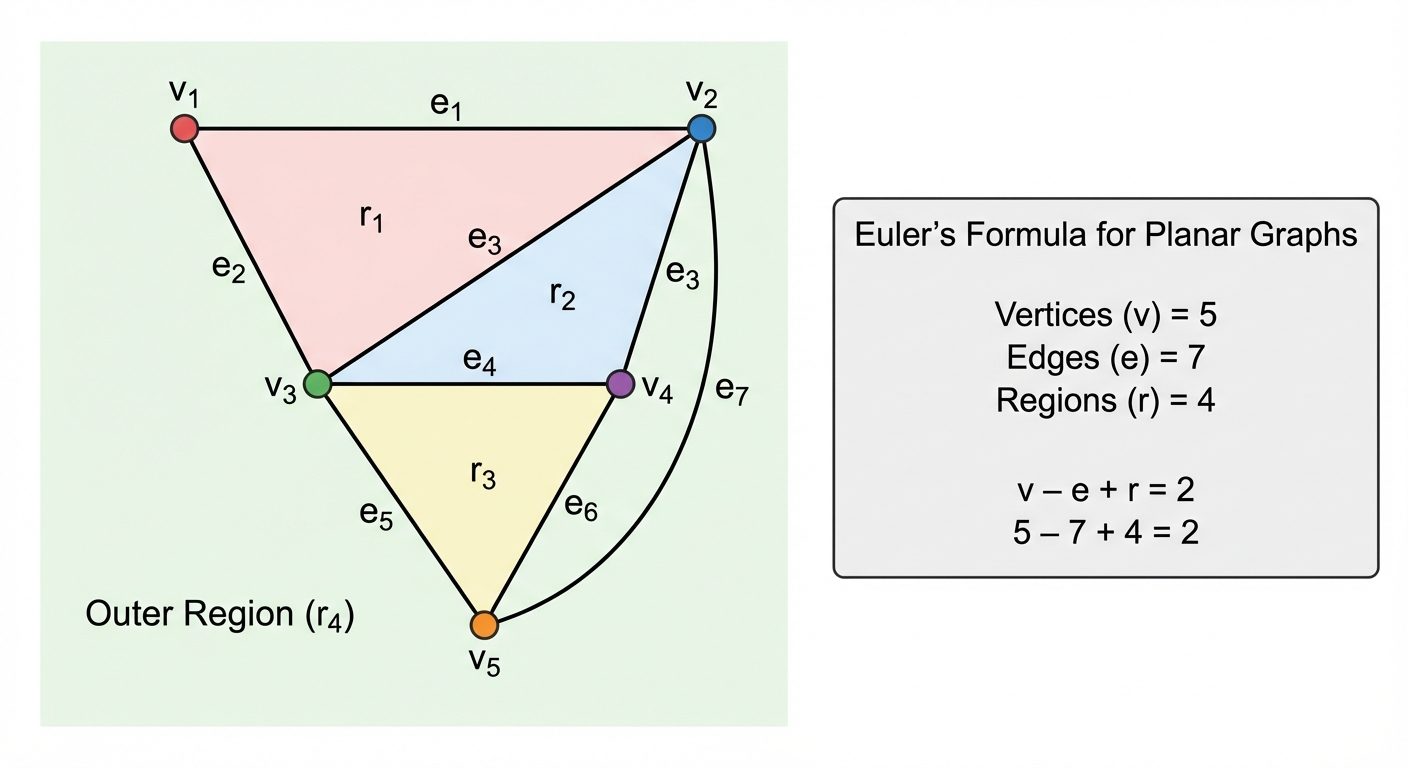
A graph is planar if it can be drawn on a 2D plane without any edges crossing each other. Such a drawing is called a planar embedding.

• Regions (Faces): A planar representation divides the plane into regions, including the unbounded (infinite) outer region.
• Kuratowski's Theorem: A graph is non-planar if and only if it contains a subgraph homeomorphic to (complete graph with 5 vertices) or (complete bipartite graph).

Euler’s Formula

For a connected planar graph with vertices, edges, and regions (faces):

Corollaries for Simple Connected Planar Graphs ():

• If the graph has no triangles (shortest cycle length ), then .

2. Graph Colouring

Graph Colouring involves assigning colors to vertices such that no two adjacent vertices share the same color.

• Chromatic Number (): The minimum number of colors required to color graph .
• k-colourable: A graph that can be colored using colors.

Key Chromatic Numbers:

• Cycle Graph (): if is even; if is odd.
• Complete Graph (): (every node connects to every other node).
• Bipartite Graph: .
• Planar Graphs: (The Four Color Theorem).

3. Trees and Their Properties

A Tree is a connected undirected graph with no simple cycles.

Fundamental Properties

For a tree with vertices:

1. It has exactly edges.
2. There is a unique simple path between any two vertices.
3. Adding any edge creates exactly one cycle.
4. Removing any edge disconnects the graph (every edge is a bridge).
5. A collection of disjoint trees is called a Forest.

Rooted Tree

A tree in which one vertex is distinguished as the Root.

• Parent/Child: If is an edge and is closer to the root, is the parent of .
• Leaf: A node with no children.
• Siblings: Nodes sharing the same parent.
• Height/Depth: The length of the path from the root to the deepest node.
• m-ary Tree: Every internal vertex has at most children. (Full m-ary tree: exactly children).

4. Spanning Trees and MST

Spanning Tree

A subgraph of a connected graph that contains all vertices of and is a tree.

• A graph may have multiple spanning trees.
• Removing edges from a cyclic graph until it is acyclic (but still connected) results in a spanning tree.

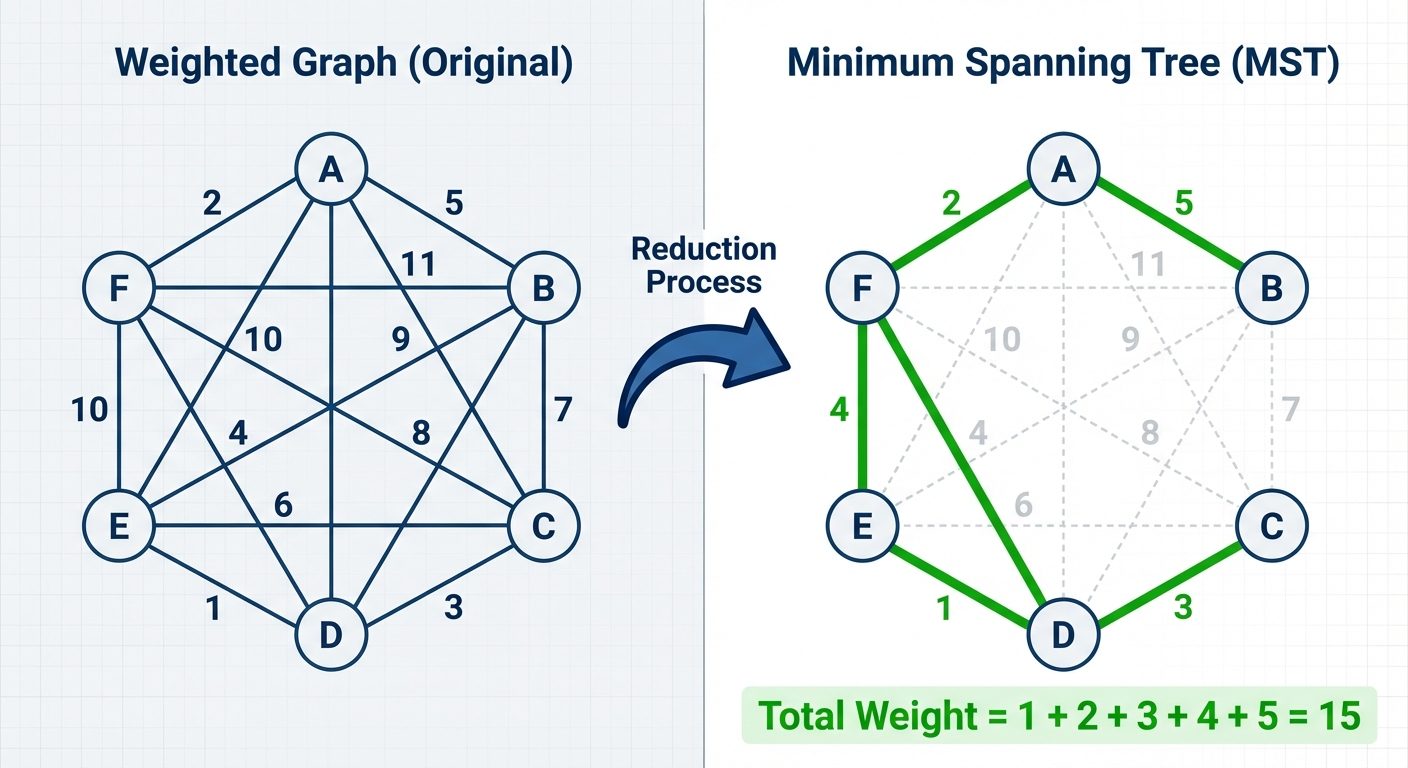
Minimum Spanning Tree (MST)

In a weighted graph, the MST is the spanning tree where the sum of edge weights is minimized.

Algorithms:

1. Prim’s Algorithm: Grow the tree from a starting vertex by always adding the cheapest edge connected to the existing tree vertices.
2. Kruskal’s Algorithm: Sort all edges by weight; add edges from smallest to largest, skipping those that form a cycle.

5. Decision Trees

A Decision Tree is a rooted tree used to model decisions and their possible consequences.

• Internal Nodes: Represent a test or a decision point.
• Branches: Represent the outcome of the test.
• Leaf Nodes: Represent the final class label or decision value.
• Application: Used in sorting algorithms (decision tree lower bound is ), game theory, and machine learning.

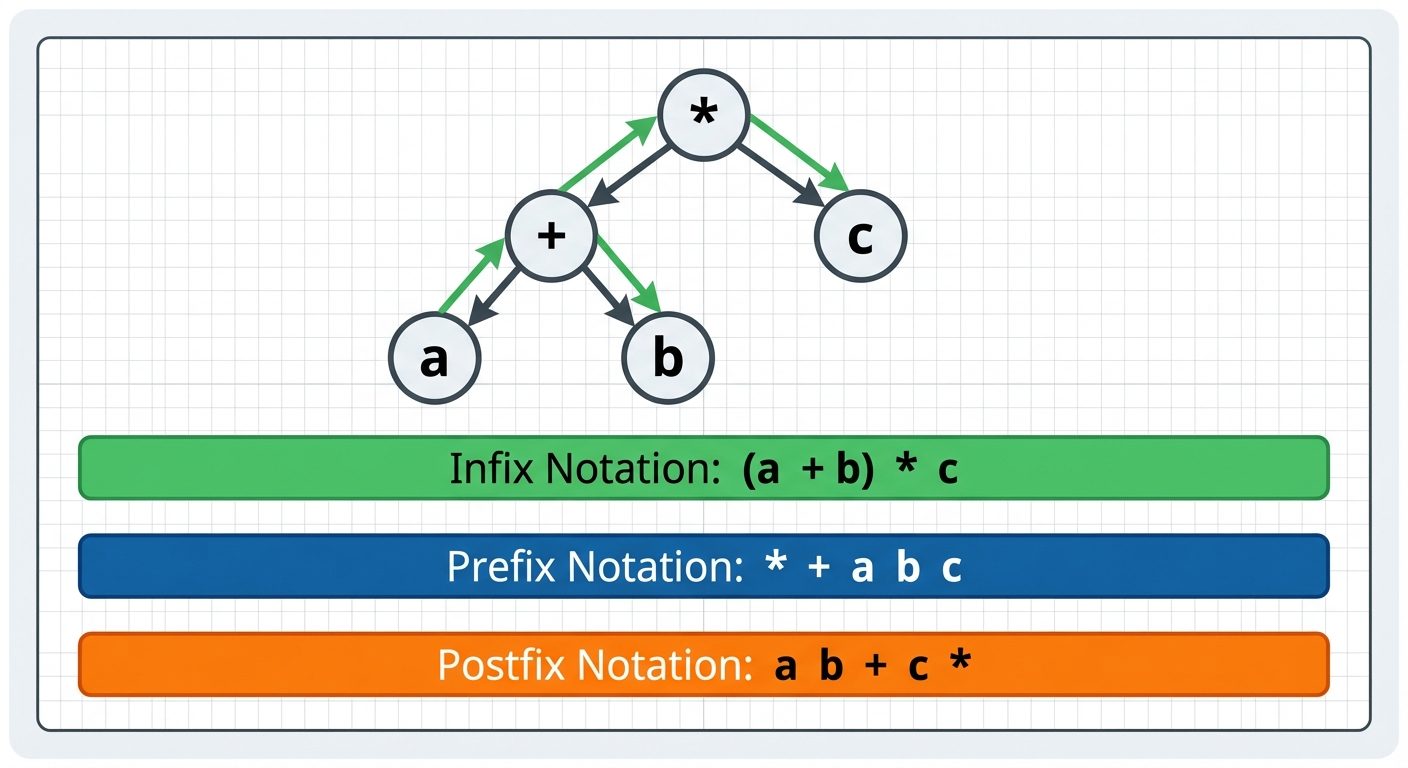
6. Tree Traversal (Notations)

Traversal refers to visiting every node in a tree exactly once. These are commonly applied to Binary Expression Trees where leaves are operands and internal nodes are operators.

1. Infix Notation (In-order Traversal)

Order: Left Child Root Right Child

• Standard arithmetic notation.
• Requires parentheses to preserve order of operations.
• Example:

2. Prefix Notation (Pre-order Traversal)

Order: Root Left Child Right Child

• Also known as Polish Notation.
• Operator precedes operands.
• No parentheses needed.
• Example:

3. Postfix Notation (Post-order Traversal)

Order: Left Child Right Child Root

• Also known as Reverse Polish Notation (RPN).
• Operator follows operands.
• Easily evaluated using a stack.
• Example: