Back to Subject

Practice MCQ Subjective

Unit 6 - Notes

MTH401 5 min read

Unit 6: Number theory and its application in cryptography

1. Divisibility and Modular Arithmetic

Divisibility

Let $a$ and $b$ be integers with $a \neq 0$ .

Definition: We say $a$ divides $b$ (denoted $a \mid b$ ) if there exists an integer $c$ such that $b = ac$ .
Properties:
- Reflexive: $a \mid a$ .
- Transitive: If $a \mid b$ and $b \mid c$ , then $a \mid c$ .
- Linearity: If $a \mid b$ and $a \mid c$ , then $a \mid (mb + nc)$ for any integers $m, n$ .

The Division Algorithm

For any integer $a$ and positive integer $d$ , there exist unique integers $q$ (quotient) and $r$ (remainder) such that:

a = dq + r, \quad 0 \leq r < d

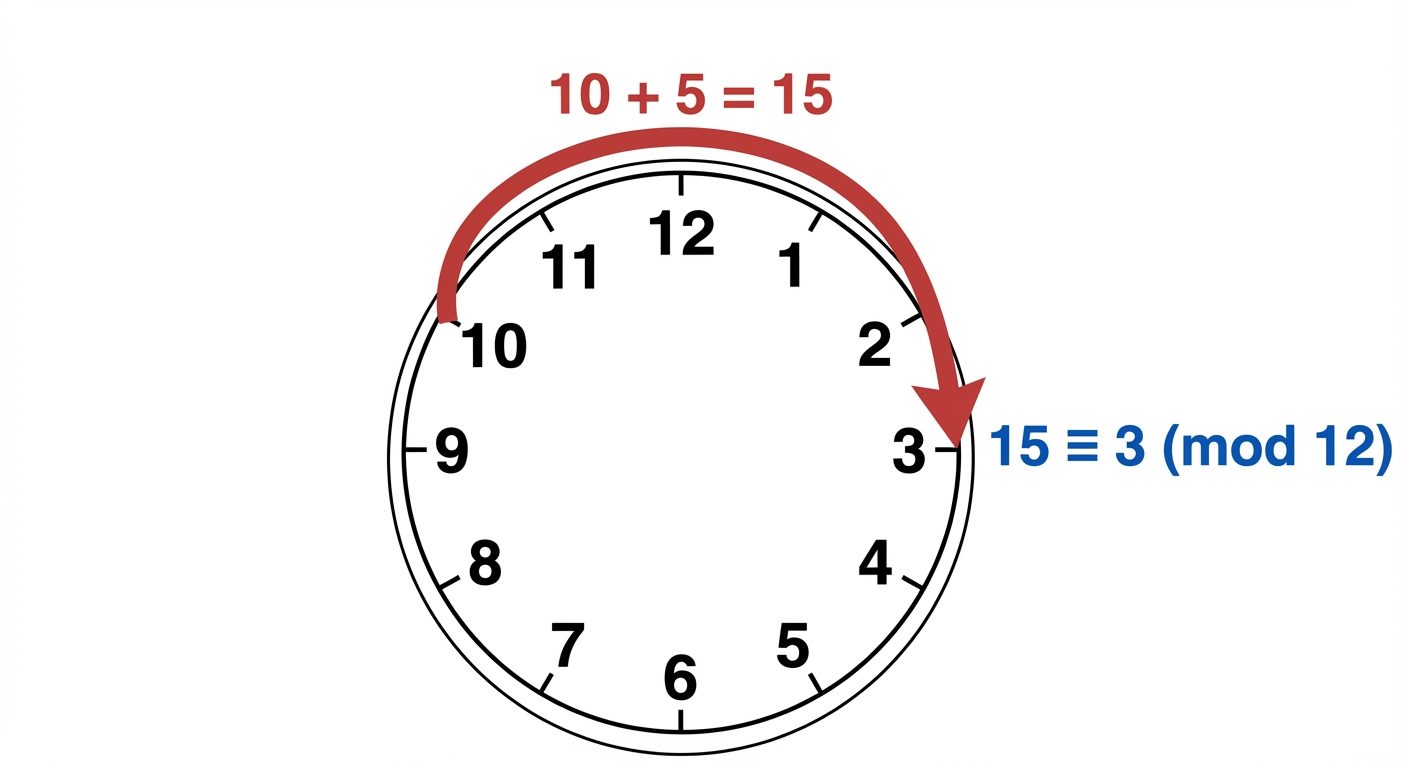
Modular Arithmetic

Definition: $a$ is congruent to $b$ modulo $m$ ( $a \equiv b \pmod m$ ) if $m$ divides $(a - b)$ .
Alternatively, $a \pmod m = b \pmod m$ (they have the same remainder when divided by $m$ ).
Arithmetic Operations:
- $(a + b) \pmod m = ((a \pmod m) + (b \pmod m)) \pmod m$
- $(a \cdot b) \pmod m = ((a \pmod m) \cdot (b \pmod m)) \pmod m$

A conceptual diagram illustrating "Clock Arithmetic" for Modulo 12. The image should feature a tradi... — AI-generated image — may contain inaccuracies

2. Primes, GCD, and LCM

Prime Numbers

Prime: An integer $p > 1$ whose only positive divisors are $1$ and $p$ .
Composite: An integer $n > 1$ that is not prime.
Fundamental Theorem of Arithmetic: Every integer $n > 1$ can be written uniquely as a product of primes (up to the order of factors).

Greatest Common Divisor (GCD)

The largest integer $d$ such that $d \mid a$ and $d \mid b$ .
Notation: $\gcd(a, b)$ .
Coprime: If $\gcd(a, b) = 1$ , $a$ and $b$ are relatively prime.

Least Common Multiple (LCM)

The smallest positive integer $m$ that is a multiple of both $a$ and $b$ .
Relationship: $a \cdot b = \gcd(a, b) \cdot \text{lcm}(a, b)$ .

3. Euclidean Algorithm and Bezout's Lemma

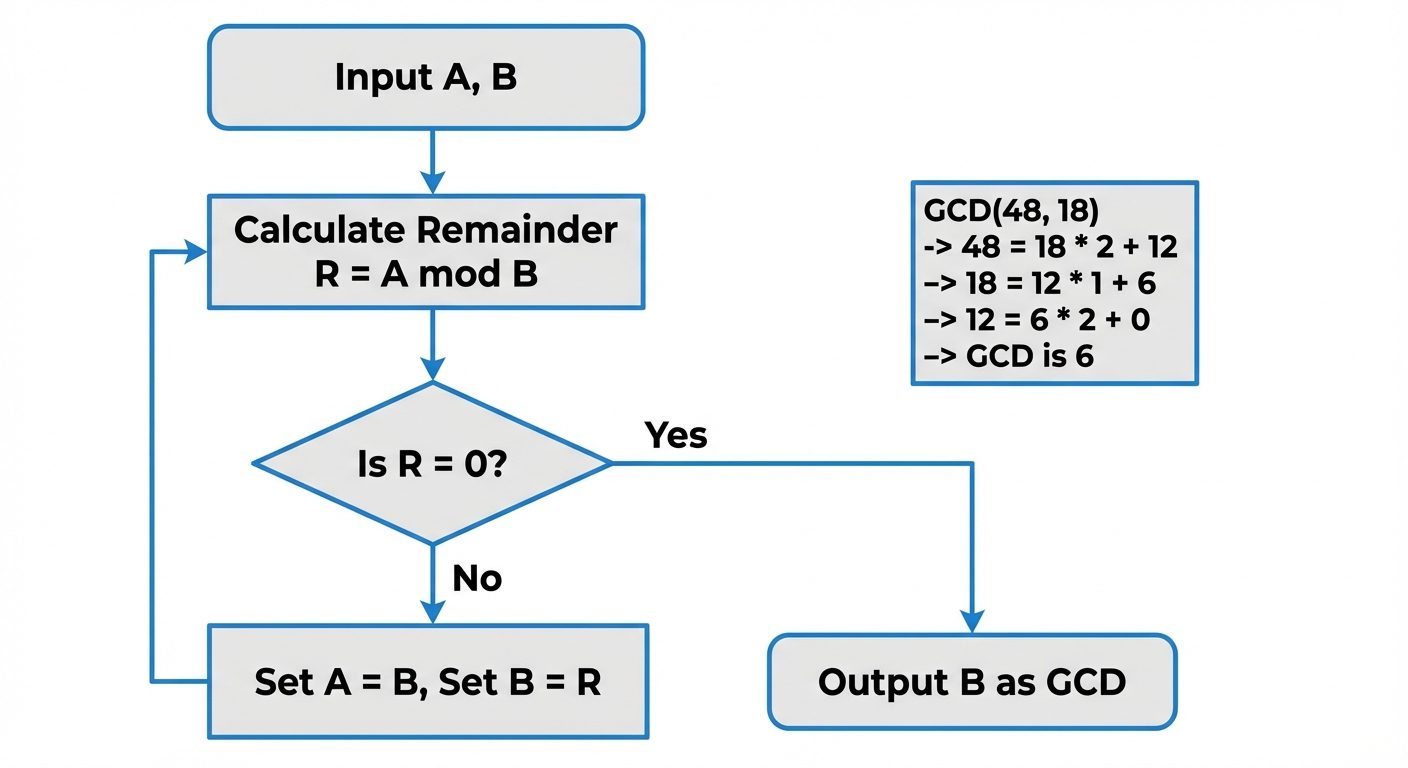
Euclidean Algorithm

An efficient method for computing $\gcd(a, b)$ without factoring. It uses successive divisions:

Let $a = bq_1 + r_1$
Let $b = r_1q_2 + r_2$
Let $r_1 = r_2q_3 + r_3$
Continue until the remainder is 0. The last non-zero remainder is the GCD.

A vertical flowchart diagram showing the steps of the Euclidean Algorithm to find GCD(A, B). Step 1 ... — AI-generated image — may contain inaccuracies

Bezout's Lemma

For any non-zero integers $a$ and $b$ , there exist integers $x$ and $y$ such that:
$ax + by = \gcd(a, b)$
$x$ and $y$ are called Bezout coefficients and can be found using the Extended Euclidean Algorithm (working backward through the Euclidean algorithm steps).

4. Linear Congruence and Inverses

Linear Congruence

An equation of the form $ax \equiv b \pmod m$ .
Solvability: A solution exists if and only if $d \mid b$ , where $d = \gcd(a, m)$ .
If solvable, there are exactly $d$ distinct solutions modulo $m$ .

Inverse of $a$ Modulo $m$

The modular multiplicative inverse of $a$ is an integer $x$ such that:
$ax \equiv 1 \pmod m$
Existence: The inverse exists if and only if $\gcd(a, m) = 1$ (i.e., $a$ and $m$ are coprime).
Typically denoted as $a^{-1}$ .

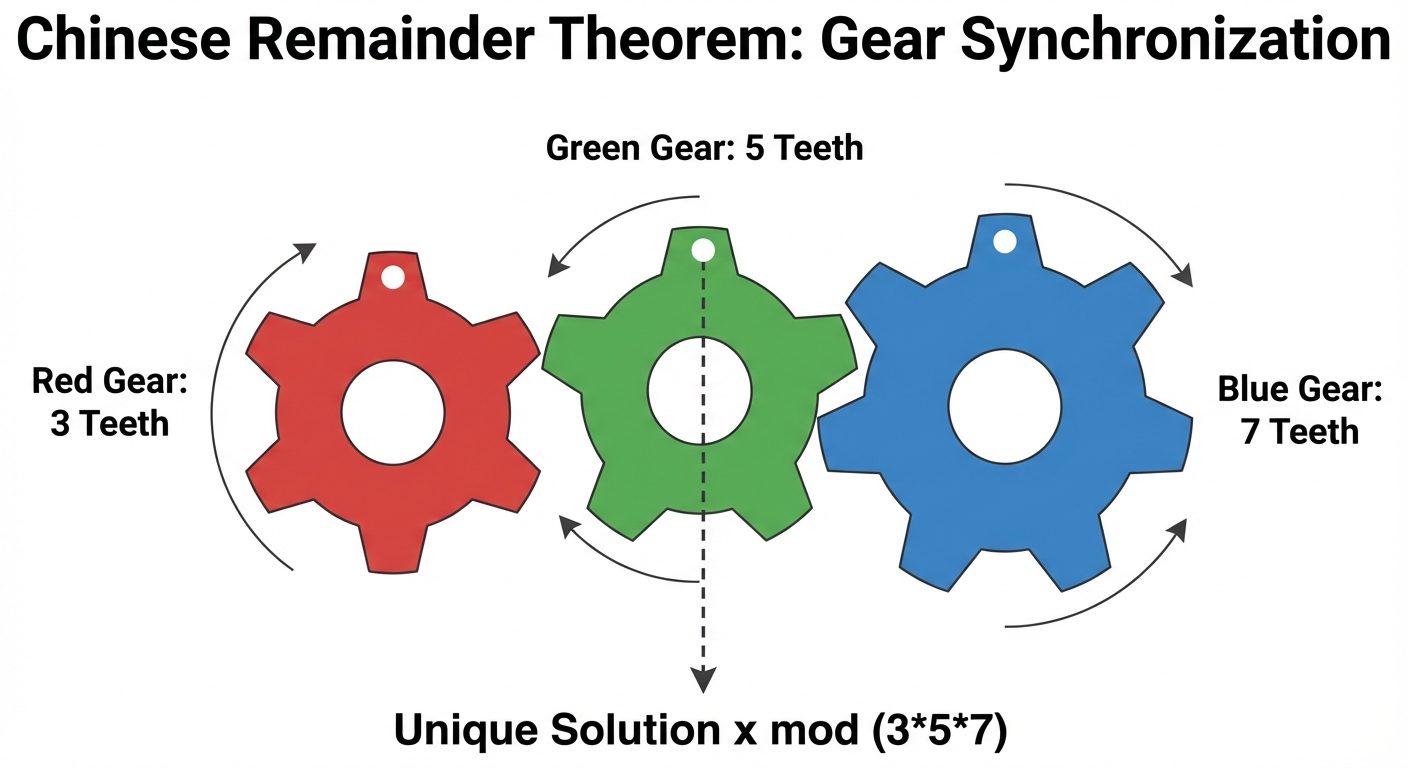
5. Chinese Remainder Theorem (CRT)

Problem: Solving a system of simultaneous congruences:
$x \equiv a_1 \pmod{m_1}$
$x \equiv a_2 \pmod{m_2}$
$...$
$x \equiv a_k \pmod{m_k}$
Theorem: If the moduli $m_1, m_2, \dots, m_k$ are pairwise relatively prime (gcd of any pair is 1), then there exists a unique solution for $x$ modulo $M = m_1 \times m_2 \times \dots \times m_k$ .
Formula:
- Where $M_i = M/m_i$
- $y_i$ is the modular inverse of $M_i$ modulo $m_i$ .

A mechanical visualization of the Chinese Remainder Theorem using gears. Show three interlocked gear... — AI-generated image — may contain inaccuracies

6. Fermat’s Little Theorem

Statement: If $p$ is a prime number and $a$ is an integer not divisible by $p$ :
$a^{p-1} \equiv 1 \pmod p$
Alternative Form: For any integer $a$ and prime $p$ :
$a^p \equiv a \pmod p$
Application: Crucial for simplifying large exponents in modular arithmetic and serves as the basis for primality testing.

7. Cryptography Applications

Basic Terminology

Plaintext ( $P$ ): Original message.
Ciphertext ( $C$ ): Encrypted message.
Key ( $K$ ): Secret information used for encryption/decryption.

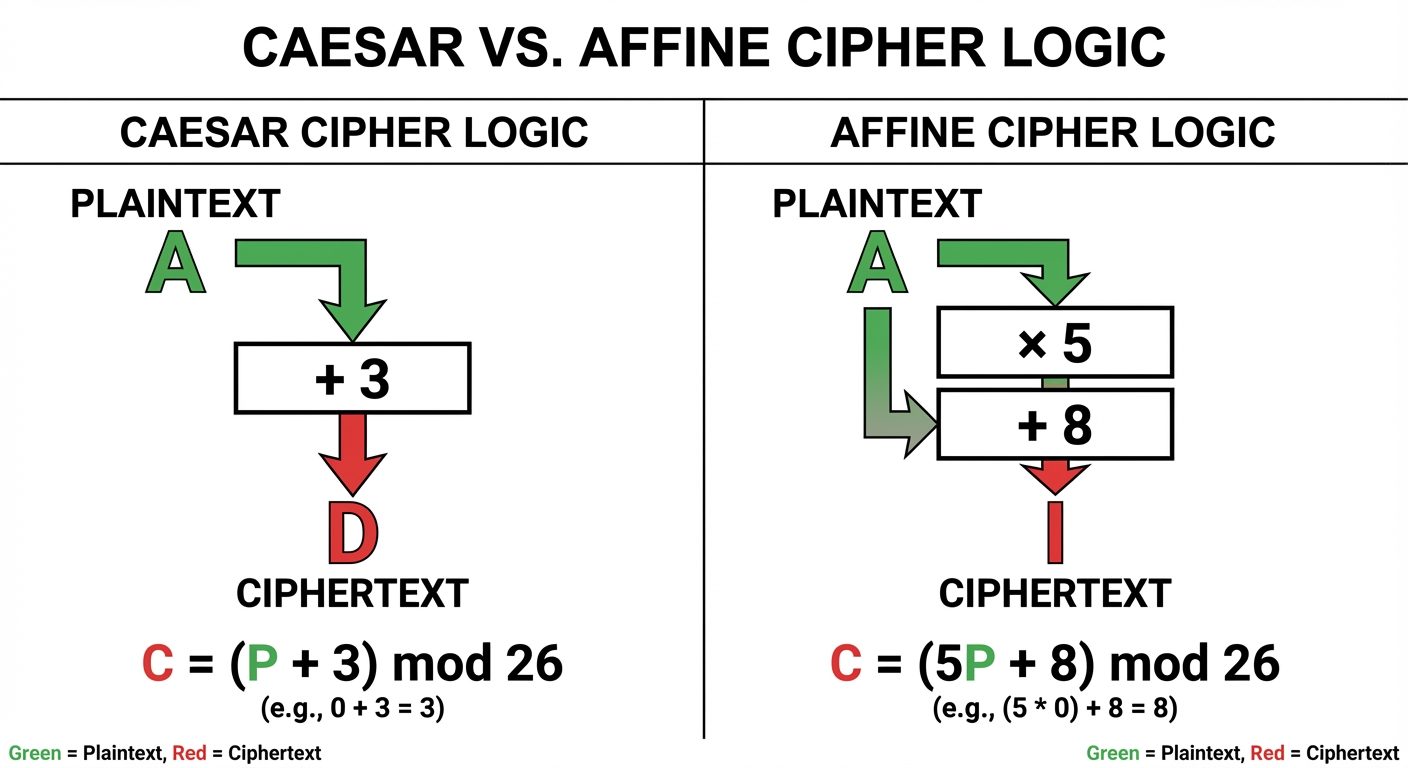
Caesar Cipher

Type: Shift Cipher (Substitution).
Encryption: Replace each letter with the letter $k$ positions down the alphabet.
$C = (P + k) \pmod{26}$
(Mapping $A=0, B=1, \dots, Z=25$ )
Decryption:
$P = (C - k) \pmod{26}$

Affine Transformation (Affine Cipher)

Encryption Function:
- $a$ : Multiplicative key (must be coprime to 26).
- $b$ : Additive shift key.
Decryption Function:
- Requires finding the modular inverse $a^{-1} \pmod{26}$ .
Security: Stronger than Caesar cipher but still vulnerable to frequency analysis.

A split-panel comparison diagram of Caesar vs. Affine Cipher logic. Left Panel (Caesar): Shows "A" e... — AI-generated image — may contain inaccuracies

Unit 5