Back to Subject

Practice MCQ Subjective

Unit 3 - Notes

MTH401 4 min read

Unit 3: Counting Principles and Relations

1. Counting Principles

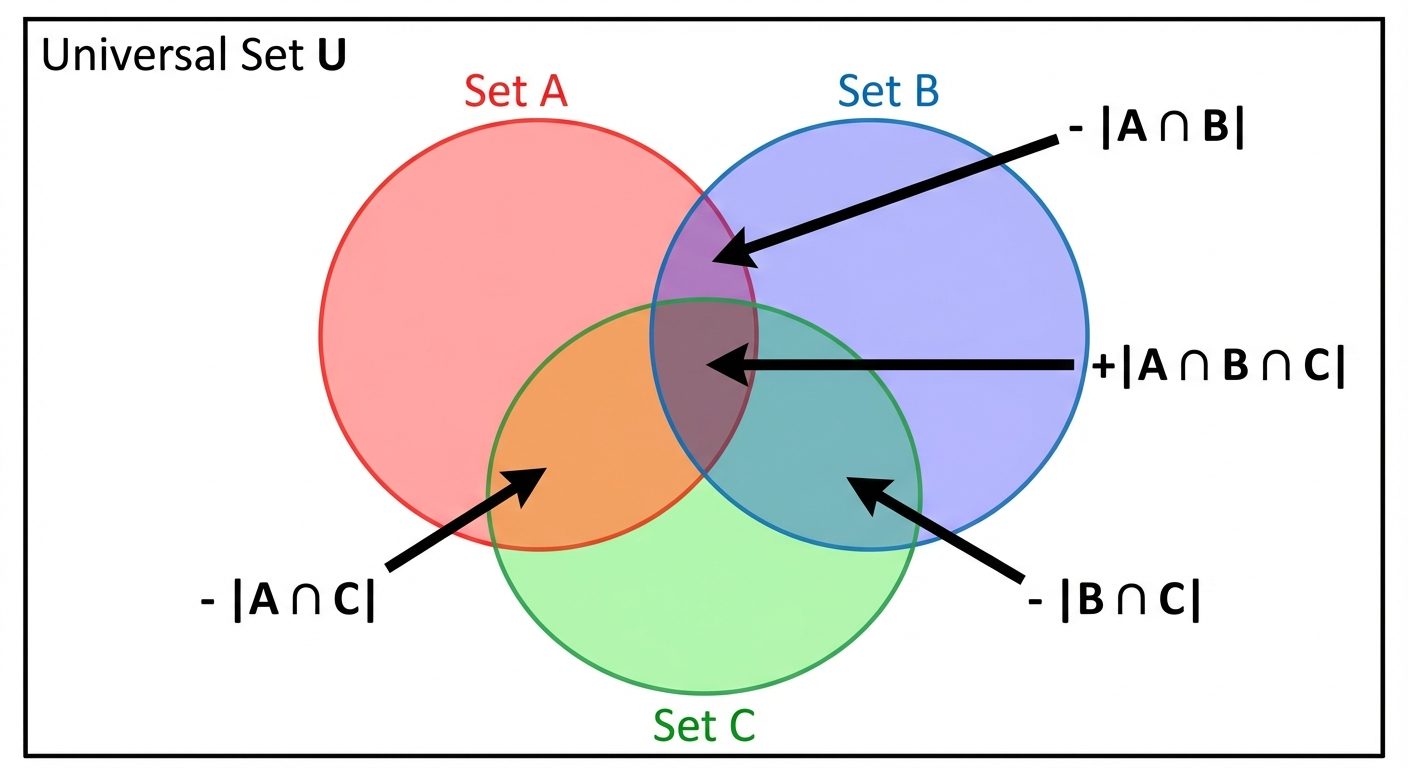
Principle of Inclusion-Exclusion (PIE)

Used to calculate the size of the union of multiple sets by accounting for overlapping elements (intersections).

For Two Sets ( $A, B$ ):
$|A \cup B| = |A| + |B| - |A \cap B|$
For Three Sets ( $A, B, C$ ):
$|A \cup B \cup C| = |A| + |B| + |C| - (|A \cap B| + |A \cap C| + |B \cap C|) + |A \cap B \cap C|$

A Venn diagram illustrating the Principle of Inclusion-Exclusion for three sets A, B, and C inside a... — AI-generated image — may contain inaccuracies

Pigeonhole Principle

Basic Principle: If $k+1$ objects are placed into $k$ boxes, then at least one box contains two or more objects.
Generalized Pigeonhole Principle: If $N$ objects are placed into $k$ boxes, then at least one box contains at least $\lceil N/k \rceil$ objects (where $\lceil x \rceil$ is the ceiling function).

2. Relations and Their Properties

A Binary Relation $R$ from set $A$ to set $B$ is a subset of the Cartesian product $A \times B$ . If $A=B$ , it is a relation on set $A$ .

Properties of Relations

Let $R$ be a relation on set $A$ :

Reflexive: $\forall a \in A, (a, a) \in R$ . (Every element relates to itself).
Symmetric: If $(a, b) \in R$ , then $(b, a) \in R$ .
Antisymmetric: If $(a, b) \in R$ and $(b, a) \in R$ , then $a = b$ . (No mutual relationship unless elements are identical).
Transitive: If $(a, b) \in R$ and $(b, c) \in R$ , then $(a, c) \in R$ .

Combining Relations

Since relations are sets, set operations apply:

Union: $R_1 \cup R_2$
Intersection: $R_1 \cap R_2$
Difference: $R_1 - R_2$
Composition ( $S \circ R$ ): Let $R \subseteq A \times B$ and $S \subseteq B \times C$ . The composition is the relation from $A$ to $C$ defined as:
$(a, c) \in S \circ R$ if $\exists b \in B$ such that $(a, b) \in R$ and $(b, c) \in S$ .

3. Representing Relations

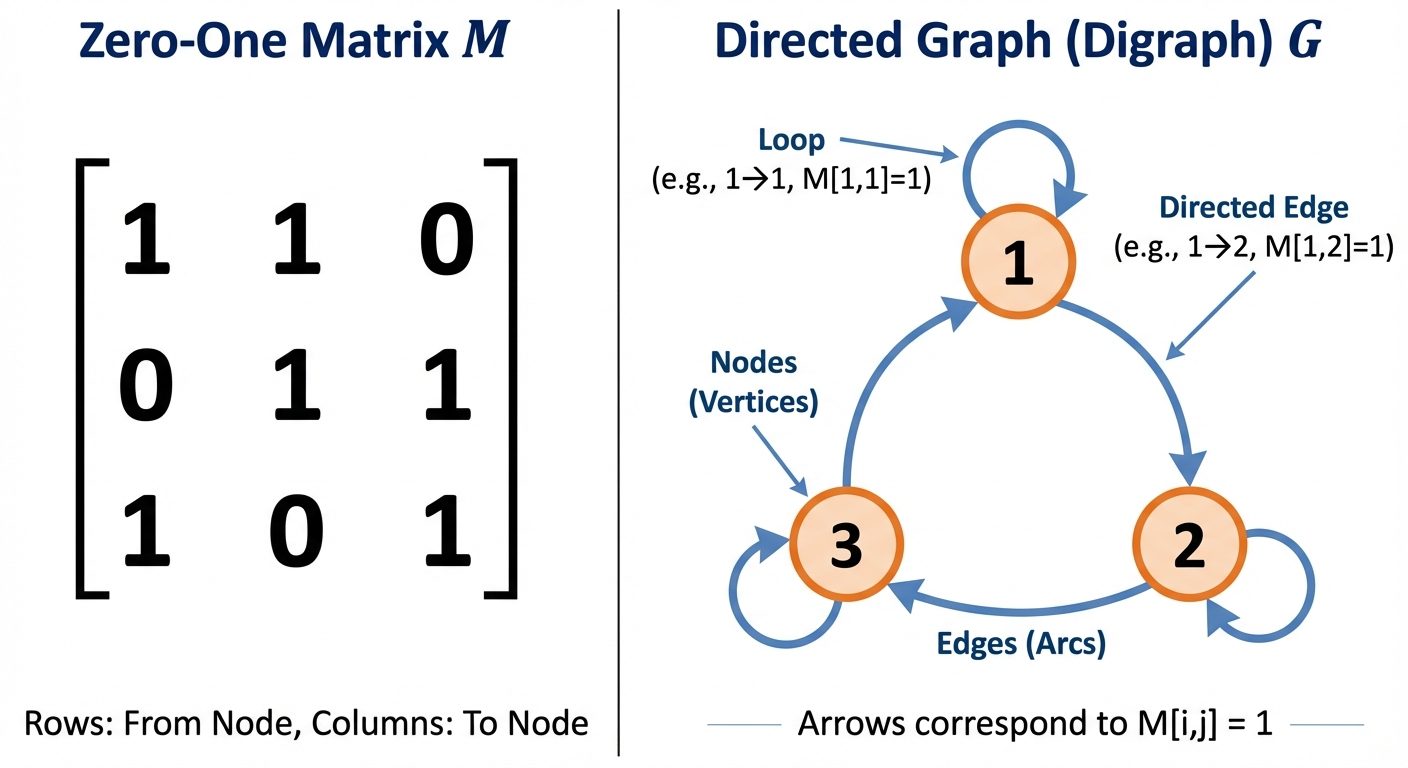
1. Zero-One Matrices

A relation $R$ on set $A = \{a_1, ..., a_n\}$ is represented by matrix $M_R = [m_{ij}]$ where:

$m_{ij} = 1$ if $(a_i, a_j) \in R$
$m_{ij} = 0$ if $(a_i, a_j) \notin R$

Properties in Matrix form:

Reflexive: Main diagonal contains all 1s.
Symmetric: Matrix is symmetric ( $M = M^T$ ).

2. Directed Graphs (Digraphs)

Vertices: Elements of set $A$ .
Edges: Directed arrow from $a$ to $b$ if $(a, b) \in R$ .
Loops: An edge from a vertex to itself (indicates Reflexivity).

A split diagram comparing two representations of the same relation. Left side: A 3x3 Zero-One Matrix... — AI-generated image — may contain inaccuracies

=1) and an arrow from 1 to 2. Label the left side "Matrix Representation" and the right side "Digraph Representation". Use clean black lines on white background.]

4. Types of Relations

Equivalence Relations

A relation $R$ is an Equivalence Relation if it is:

Reflexive
Symmetric
Transitive

Equivalence Class $[a]$ : The set of all elements related to $a$ . These classes partition the set $A$ .

Partial Ordering Relations (POSET)

A relation $R$ is a Partial Order if it is:

Reflexive
Antisymmetric
Transitive

Notation: $(S, \preceq)$ denotes a POSET.
Comparable: Two elements $a, b$ are comparable if $a \preceq b$ or $b \preceq a$ .
Total Ordering: A POSET where every pair of elements is comparable (a linear chain).

5. Lattices and Hasse Diagrams

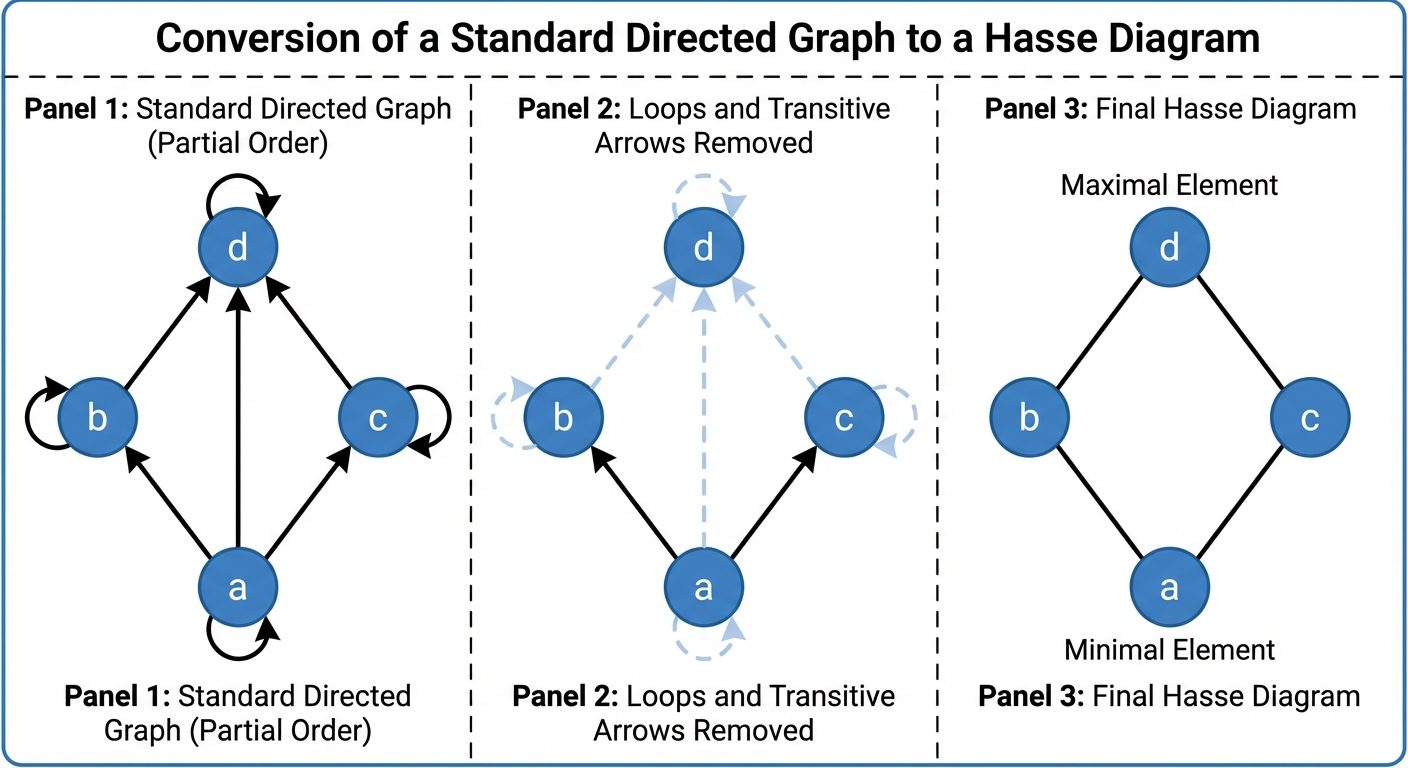
Hasse Diagrams

A simplified graphical representation of a finite POSET.

Rules for Construction:
1. Remove all self-loops (Reflexivity is implied).
2. Remove transitive edges (If $a \to b$ and $b \to c$ , remove $a \to c$ ).
3. Arrangement implies direction: If $a \preceq b$ , place $b$ physically higher than $a$ . Remove arrows; lines connect elements.

Components of a Hasse Diagram

Maximal Element: No element is "above" it.
Minimal Element: No element is "below" it.
Greatest Element (Maximum): Unique element greater than all others.
Least Element (Minimum): Unique element less than all others.
Upper Bound: An element $x$ such that $x \succeq a$ and $x \succeq b$ .
Lower Bound: An element $x$ such that $x \preceq a$ and $x \preceq b$ .

A step-by-step diagram showing the conversion of a standard directed graph to a Hasse diagram. Panel... — AI-generated image — may contain inaccuracies

Lattice

A Lattice is a POSET $(L, \preceq)$ in which every pair of elements has both:

Least Upper Bound (LUB/Supremum/Join): Notation $a \lor b$ .
Greatest Lower Bound (GLB/Infimum/Meet): Notation $a \land b$ .

Sub Lattice

A non-empty subset $M$ of a lattice $L$ is a sub lattice if $M$ itself is a lattice under the same operations ( $\lor$ and $\land$ ) defined in $L$ .

If $a, b \in M$ , then $a \lor b \in M$ and $a \land b \in M$ .

Unit 2

Unit 4