Unit 2 - Notes

MTH401 5 min read

Unit 2: Recurrence Relations

1. Introduction to Recurrence Relations

Definition

A recurrence relation for a sequence $a_0, a_1, a_2, \dots$ is an equation that relates the $n$ -th term, $a_n$ , to one or more of its predecessors ( $a_{n-1}, a_{n-2}, \dots$ ).

Order: The difference between the highest and lowest subscripts of the terms present in the relation.
Solution: A sequence that satisfies the recurrence relation.
Initial Conditions: Specific values given for the first few terms (e.g., $a_0 = 1$ ) required to find a unique solution.

Modelling with Recurrence Relations

Recurrence relations are used to model problems where the state at step $n$ depends on the state at previous steps.

Compound Interest: $P_n = (1 + r)P_{n-1}$
Fibonacci Sequence: $F_n = F_{n-1} + F_{n-2}$ (modelling rabbit populations).
Tower of Hanoi: $H_n = 2H_{n-1} + 1$ .

2. Homogeneous Linear Recurrence Relations (Constant Coefficients)

Standard Form

A linear homogeneous recurrence relation of degree $k$ with constant coefficients is:

a_n = c_1 a_{n-1} + c_2 a_{n-2} + \dots + c_k a_{n-k}

Where

c_1, c_2, \dots, c_k

are real constants and

c_k \neq 0

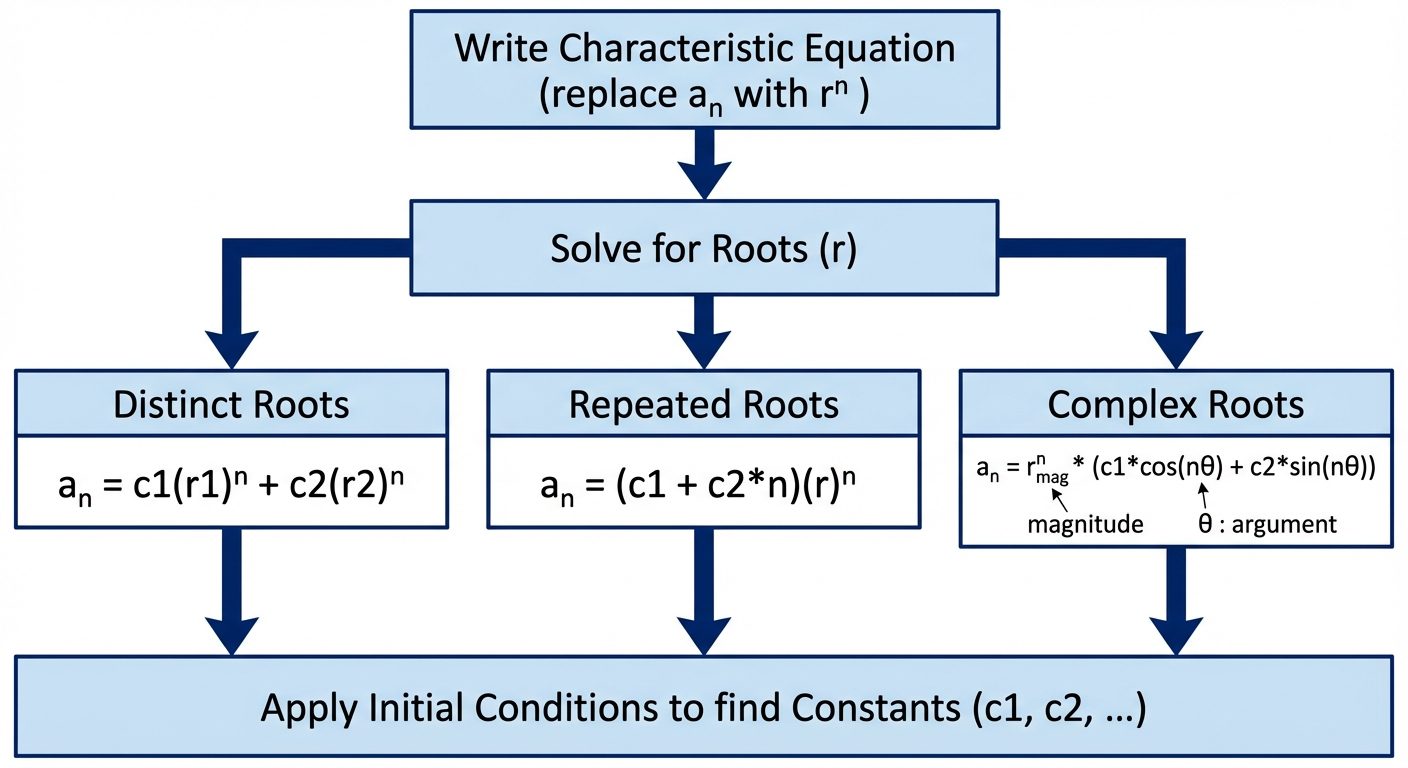
Method of Solution (Characteristic Roots)

Form the Characteristic Equation: Replace $a_n$ with $r^n$ .

$r^k - c_1 r^{k-1} - c_2 r^{k-2} - \dots - c_k = 0$
Find the Roots: Solve for $r$ .
Write the General Solution:

Nature of Roots Form of Solution ( $a_n^{(h)}$ )

Distinct Real Roots ( $r_1 \neq r_2 \dots$ ) $a_n = A(r_1)^n + B(r_2)^n + \dots$

Repeated Real Roots ( $r_1$ repeated $m$ times) $a_n = (A_1 + A_2n + \dots + A_m n^{m-1})r_1^n$

Complex Roots ( $\alpha \pm i\beta$ ) $a_n = \rho^n (A \cos(n\theta) + B \sin(n\theta))$
where $\rho = \sqrt{\alpha^2+\beta^2}, \theta = \tan^{-1}(\frac{\beta}{\alpha})$
Find Constants: Use initial conditions to solve for $A, B, \dots$ .

A detailed vertical flowchart diagram illustrating the algorithm for solving Linear Homogeneous Recu... — AI-generated image — may contain inaccuracies

3. Non-Homogeneous Relations: Method of Inverse Operator

Standard Form

f(E)a_n = R(n)

Where

E

is the shift operator such that

E a_n = a_{n+1}

and

E^k a_n = a_{n+k}

General Solution structure

a_n = a_h + a_p

$a_h$ (Homogeneous Solution): Solved by setting $R(n) = 0$ (see section 2).
$a_p$ (Particular Solution): Calculated as $a_p = \frac{1}{f(E)} R(n)$ .

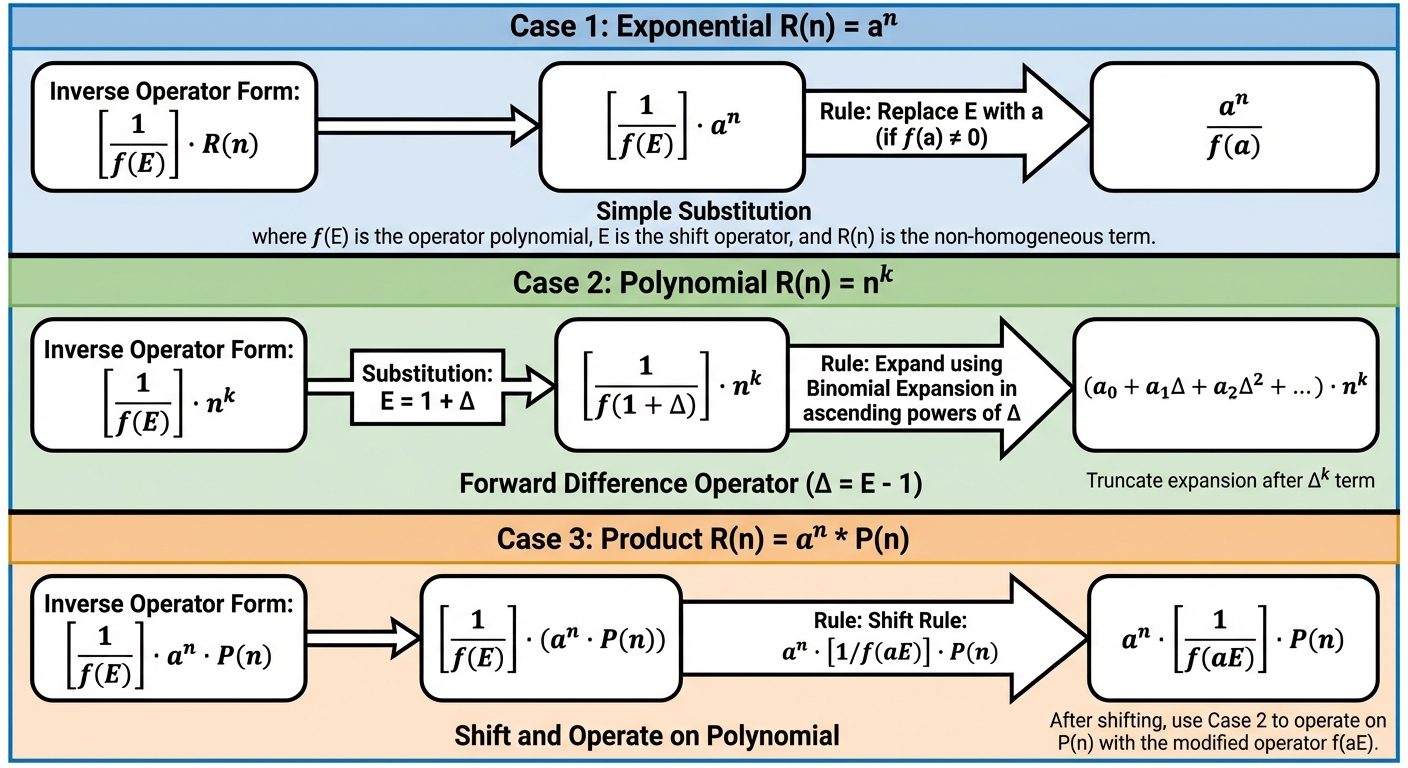
Inverse Operator Rules for Particular Solutions

The particular solution depends on the form of $R(n)$ :

Case 1: Exponential Form $R(n) = \alpha^n$

If $f(\alpha) \neq 0$ : $\frac{1}{f(E)} \alpha^n = \frac{1}{f(\alpha)} \alpha^n$
If $f(\alpha) = 0$ (Case of failure): Differentiate $f(E)$ with respect to $E$ .
$\frac{1}{(E-\alpha)^k} \alpha^n = \frac{n(n-1)\dots(n-k+1)}{k! \alpha^k} \alpha^n$ (typically approximated as $\frac{n^k}{k!}\alpha^{n-k}$ )

Case 2: Polynomial Form $R(n) = n^k$

Convert $f(E)$ to terms of $\Delta$ (where $E = 1 + \Delta$ ).
Expand $[f(1+\Delta)]^{-1}$ using Binomial expansion up to term $\Delta^k$ .
Apply the expanded operator to $n^k$ .

Case 3: Product Form $R(n) = \alpha^n \cdot P(n)$

$\frac{1}{f(E)} (\alpha^n P(n)) = \alpha^n \frac{1}{f(\alpha E)} P(n)$
This shifts $\alpha^n$ out and changes $E$ to $\alpha E$ in the denominator.

A structured block diagram or cheat sheet visual summarizing the Inverse Operator Rules for Non-Homo... — AI-generated image — may contain inaccuracies

* P(n)". Use distinct colors for each case (e.g., green, orange, purple) with mathematical formulas clearly rendered in bold black text.]

4. Generating Functions

Definition

The generating function for a sequence $a_0, a_1, a_2, \dots$ is the infinite series:

G(x) = \sum_{n=0}^{\infty} a_n x^n = a_0 + a_1 x + a_2 x^2 + \dots

Important Series Expansions

Memorizing these is crucial for solving recurrences:

Geometric Series: $\frac{1}{1-x} = \sum_{n=0}^{\infty} x^n = 1 + x + x^2 + \dots$
Binomial (Negative exponent): $\frac{1}{(1-x)^k} = \sum_{n=0}^{\infty} \binom{n+k-1}{k-1} x^n$
Specific Case ( $k=2$ ): $\frac{1}{(1-x)^2} = \sum_{n=0}^{\infty} (n+1) x^n$

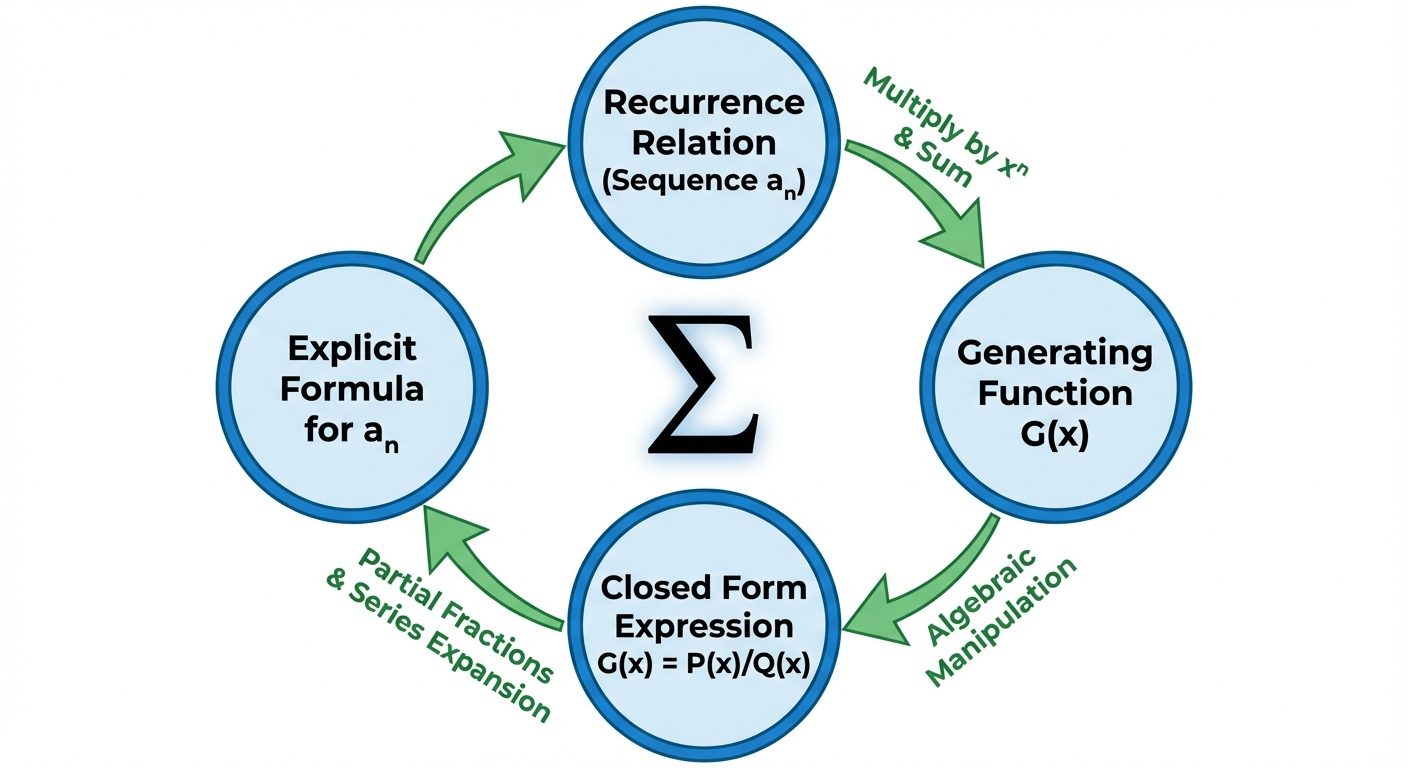
5. Solving Recurrence Relations using Generating Functions

This method converts the recurrence relation into an algebraic equation.

The Algorithm

Multiply & Sum: Multiply the recurrence relation by $x^n$ and sum from $n=k$ (where $k$ is the order) to $\infty$ .
Substitute G(x):
- Replace $\sum_{n=0}^{\infty} a_n x^n$ with $G(x)$ .
- Shift indices for terms like $a_{n-1}$ to express them in terms of $x G(x)$ .
- Example: $\sum_{n=1}^{\infty} a_{n-1} x^n = x \sum_{n=1}^{\infty} a_{n-1} x^{n-1} = x G(x)$ .
Solve Algebraically: Rearrange the equation to solve explicitly for $G(x)$ . The result is usually a rational function (fraction of polynomials).
Extract Coefficients: Use Partial Fraction Decomposition and known series expansions to find the coefficient of $x^n$ , which is $a_n$ .

A cycle diagram illustrating the "Method of Generating Functions". Four circular nodes connected in ... — AI-generated image — may contain inaccuracies

Example Setup

Given: $a_n - 3a_{n-1} = 0, a_0 = 2$ .

Multiply by $x^n$ : $\sum a_n x^n - 3 \sum a_{n-1} x^n = 0$ .
Shift: $(G(x) - a_0) - 3xG(x) = 0$ .
Solve: $G(x)(1 - 3x) = 2 \implies G(x) = \frac{2}{1-3x}$ .
Expand: $G(x) = 2 \sum (3x)^n = \sum 2(3^n)x^n$ .
Result: $a_n = 2 \cdot 3^n$ .

Unit 1

Unit 3

Nature of Roots	Form of Solution ( $a_n^{(h)}$ )
Distinct Real Roots ( $r_1 \neq r_2 \dots$ )	$a_n = A(r_1)^n + B(r_2)^n + \dots$
Repeated Real Roots ( $r_1$ repeated $m$ times)	$a_n = (A_1 + A_2n + \dots + A_m n^{m-1})r_1^n$
Complex Roots ( $\alpha \pm i\beta$ )	$a_n = \rho^n (A \cos(n\theta) + B \sin(n\theta))$ where $\rho = \sqrt{\alpha^2+\beta^2}, \theta = \tan^{-1}(\frac{\beta}{\alpha})$

Unit 2 - Notes

Table of Contents

Unit 2: Recurrence Relations

1. Introduction to Recurrence Relations

Definition

Modelling with Recurrence Relations

2. Homogeneous Linear Recurrence Relations (Constant Coefficients)

Standard Form

Method of Solution (Characteristic Roots)

3. Non-Homogeneous Relations: Method of Inverse Operator

Standard Form

General Solution structure

Inverse Operator Rules for Particular Solutions

4. Generating Functions

Definition

Important Series Expansions

5. Solving Recurrence Relations using Generating Functions

The Algorithm

Example Setup