Back to Subject

Practice MCQ Subjective

Unit 1 - Notes

MTH401 4 min read

Unit 1: Logic and Proofs

1. Propositional Logic

Propositions are declarative statements that are either True (T) or False (F), but not both.

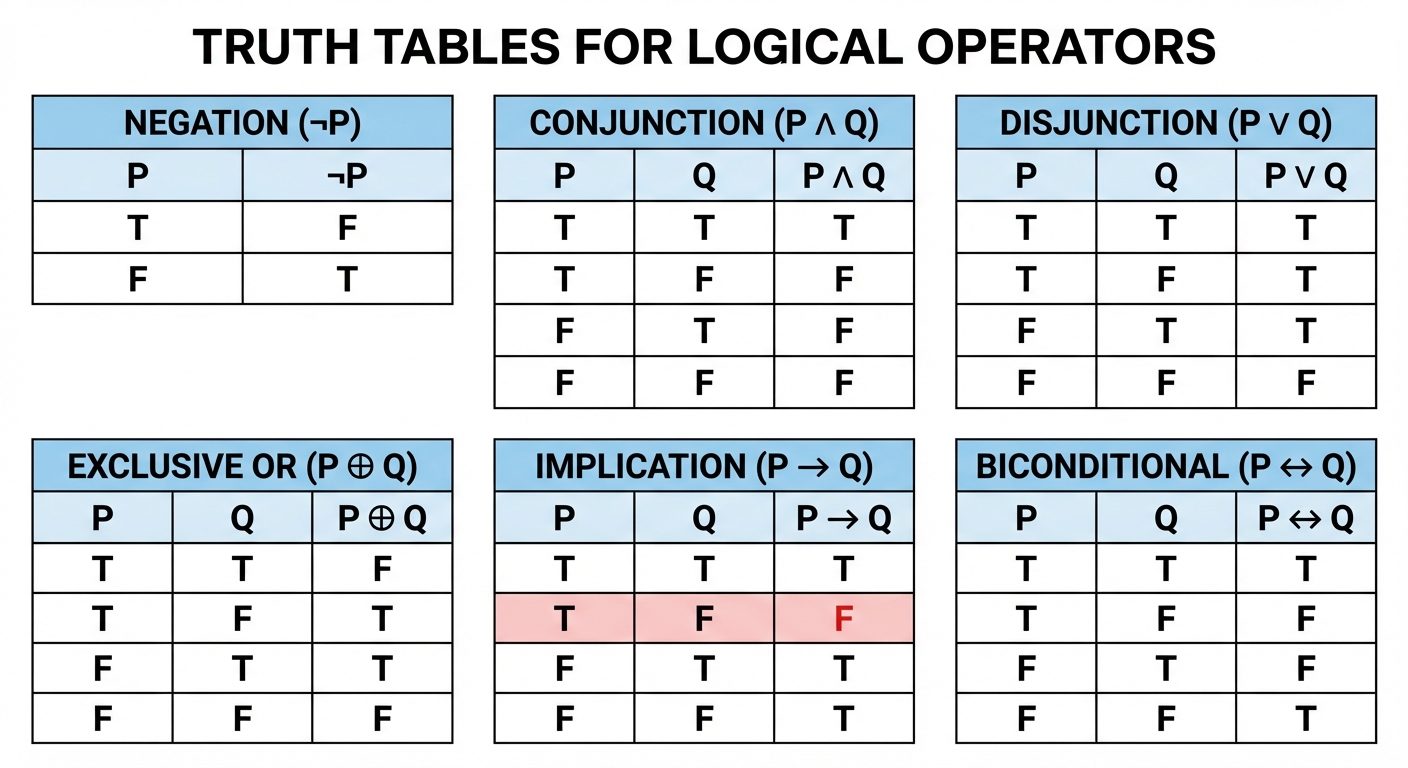
Logical Operators (Connectives)

Negation ( $\neg p$ ): "Not $p$ ". Reverses the truth value.
Conjunction ( $p \land q$ ): "And". True only if both $p$ and $q$ are true.
Disjunction ( $p \lor q$ ): "Or" (Inclusive). True if at least one is true.
Exclusive Or ( $p \oplus q$ ): "XOR". True if exactly one is true, but not both.
Implication ( $p \rightarrow q$ ): "If , then ".
- $p$ : Hypothesis/Antecedent.
- $q$ : Conclusion/Consequent.
- False only when $p$ is True and $q$ is False.
Biconditional ( $p \leftrightarrow q$ ): " $p$ if and only if $q$ ". True when $p$ and $q$ share the same truth value.

A clean, educational composite graphic displaying Truth Tables for the six main logical operators. T... — AI-generated image — may contain inaccuracies

2. Propositional Equivalences

Two compound propositions are logically equivalent ( $p \equiv q$ ) if they have the same truth values in all possible cases.

Types of Compound Propositions

Tautology: Always True (e.g., $p \lor \neg p$ ).
Contradiction: Always False (e.g., $p \land \neg p$ ).
Contingency: Neither a tautology nor a contradiction.

Key Laws of Logic

Identity & Domination Laws: $p \land T \equiv p$ ; $p \land F \equiv F$ .
De Morgan’s Laws:
1. $\neg(p \land q) \equiv \neg p \lor \neg q$
2. $\neg(p \lor q) \equiv \neg p \land \neg q$
Implication Law: $p \rightarrow q \equiv \neg p \lor q$
Contrapositive Law: $p \rightarrow q \equiv \neg q \rightarrow \neg p$

3. Predicates and Quantifiers

Predicate Logic deals with statements involving variables. $P(x)$ is a propositional function.

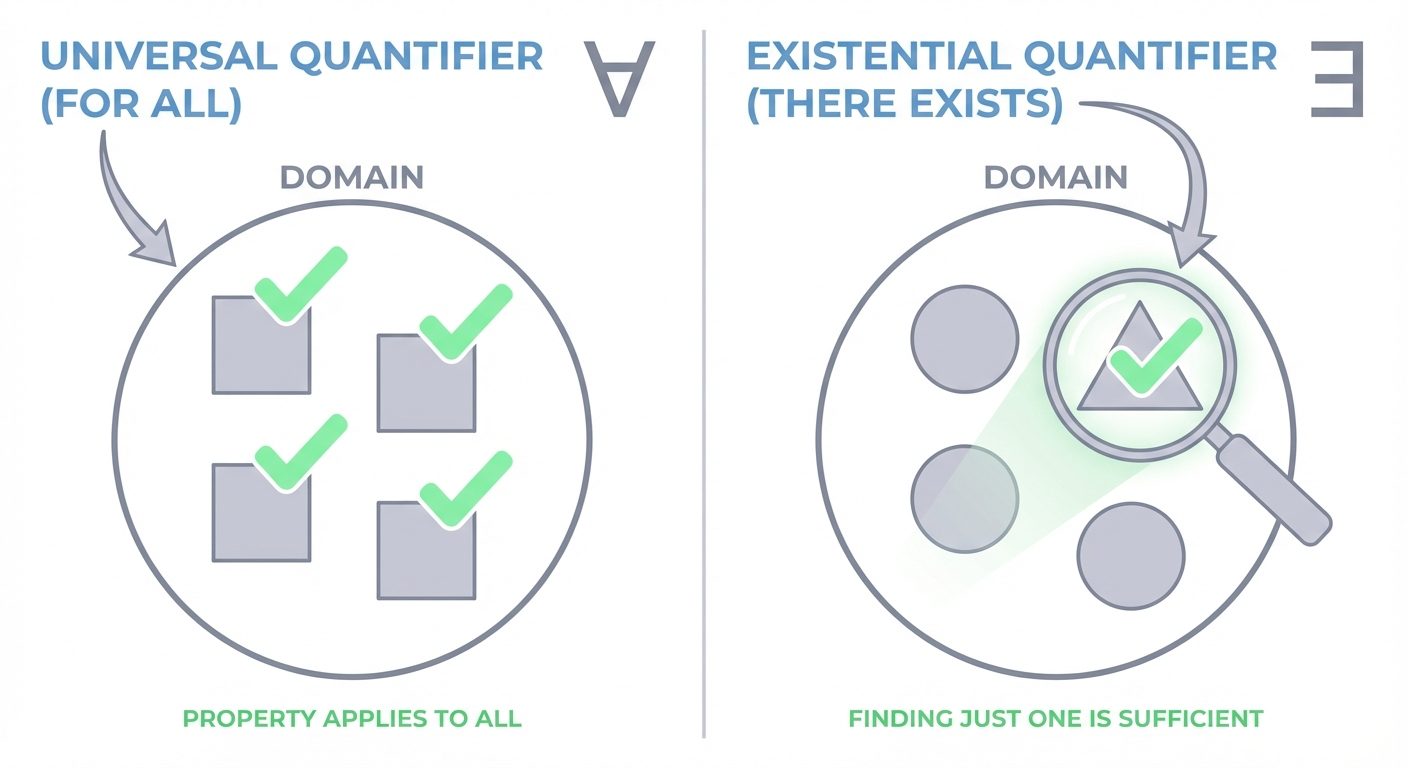
Quantifiers

Universal Quantifier ( $\forall x P(x)$ ): "For all , is true."
- True if $P(x)$ is valid for every element in the domain.
- False if there is at least one counterexample.
Existential Quantifier ( $\exists x P(x)$ ): "There exists an such that is true."
- True if $P(x)$ is valid for at least one element.
- False if $P(x)$ is false for every element.

Negating Quantifiers (De Morgan's Laws for Quantifiers)

$\neg \forall x P(x) \equiv \exists x \neg P(x)$
$\neg \exists x P(x) \equiv \forall x \neg P(x)$

A conceptual comparison illustration between the Universal and Existential quantifiers using set dia... — AI-generated image — may contain inaccuracies

4. Introduction to Proofs

A proof is a valid argument that establishes the truth of a mathematical statement.

Theorem: A statement that can be shown to be true.
Lemma: A helper theorem used to prove a larger theorem.
Corollary: A result that follows directly from a theorem.
Conjecture: A statement proposed to be true but not yet proven.

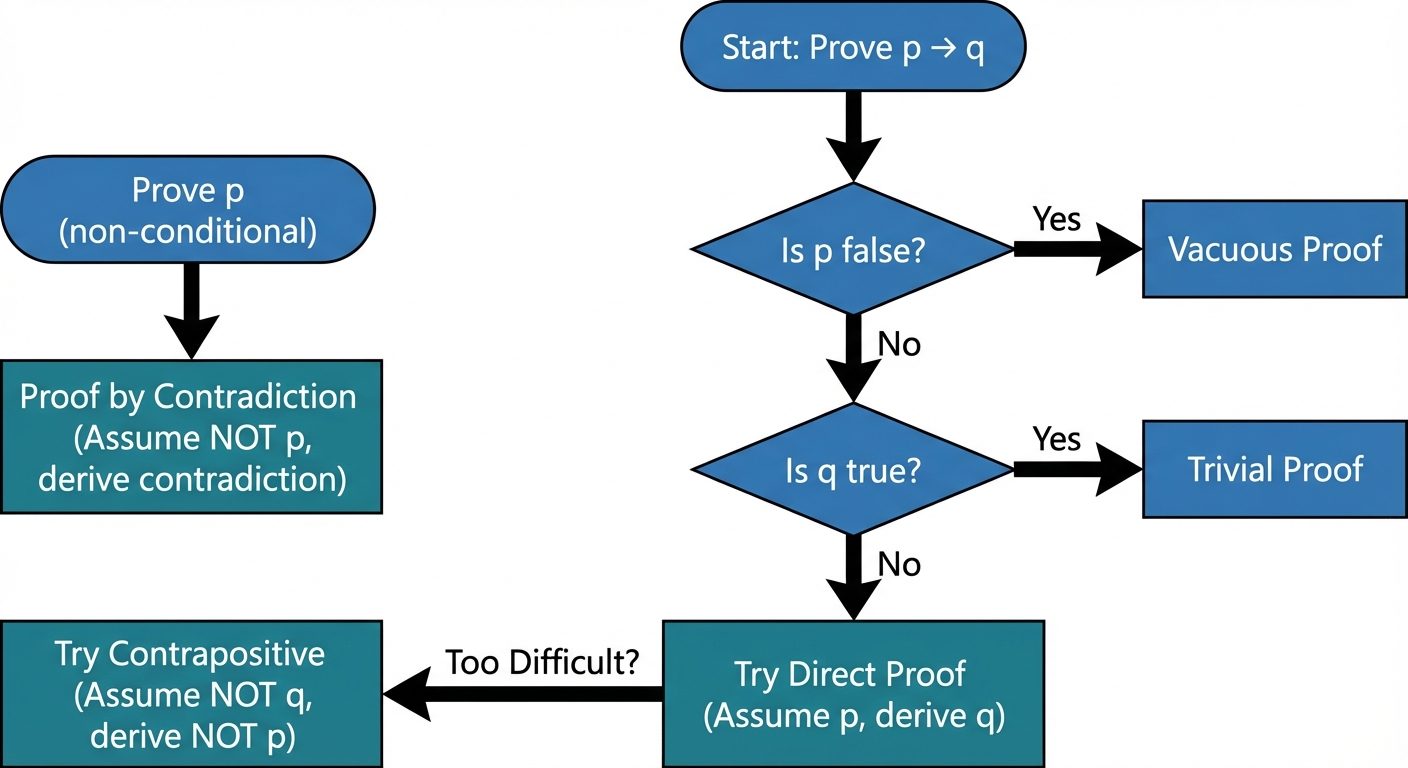
5. Methods of Proof

Direct Proof

Goal: Prove $p \rightarrow q$ .
Method: Assume $p$ is True. Use axioms, definitions, and logical steps to show that $q$ must also be True.

Proof by Contraposition (Indirect)

Goal: Prove $p \rightarrow q$ .
Method: Prove the logically equivalent contrapositive .
1. Assume $\neg q$ is True (q is false).
2. Show that $\neg p$ must be True (p is false).

Vacuous and Trivial Proofs

Vacuous Proof: Used for $p \rightarrow q$ . If we show $p$ is False, the implication is automatically True.
Trivial Proof: Used for $p \rightarrow q$ . If we show $q$ is True, the implication is automatically True regardless of $p$ .

6. Advanced Proof Strategies

Proof by Contradiction

Goal: Prove proposition $p$ is True.
Method:
1. Assume $\neg p$ is True (assume the statement is false).
2. Derive a logical contradiction (e.g., $r \land \neg r$ or $1 = 0$ ).
3. Conclude that since the assumption led to a contradiction, $\neg p$ must be False, so $p$ is True.

A flowchart diagram illustrating the decision-making process for "Choosing a Proof Strategy". The fl... — AI-generated image — may contain inaccuracies

Proof of Equivalence

Goal: Prove $p \leftrightarrow q$ .
Method: You must prove two parts:
1. $p \rightarrow q$
2. $q \rightarrow p$

Counterexamples

Goal: Disprove a universal statement $\forall x P(x)$ .
Method: Find a single element $c$ in the domain where $P(c)$ is False.

7. Mistakes in Proofs (Fallacies)

Common logical errors that invalidate a proof:

Affirming the Consequent:
- Error: $p \rightarrow q$ is true, and $q$ is true. Therefore, $p$ is true. (Invalid)
- Example: "If it rains, the ground is wet. The ground is wet, therefore it rained." (False; could be a sprinkler).
Denying the Antecedent:
- Error: $p \rightarrow q$ is true, and $p$ is false. Therefore, $q$ is false. (Invalid)
Begging the Question (Circular Reasoning):
- Using the statement you are trying to prove as one of the steps in the proof.

Unit 2