Unit 4: Arrays in C

1. Introduction to Arrays

An array is a fixed-size collection of elements of the same data type stored in contiguous memory locations. It allows a programmer to store multiple values under a single variable name, accessed using an index.

Key Characteristics

• Homogeneous: All elements must be of the same type (e.g., all integers or all floats).
• Contiguous Memory: Elements are stored side-by-side in memory.
• Indexing: Access is done via zero-based indexing (0 to size-1).
• Fixed Size: The size of the array must be known at compile time (in standard C89/90) or allocated dynamically.

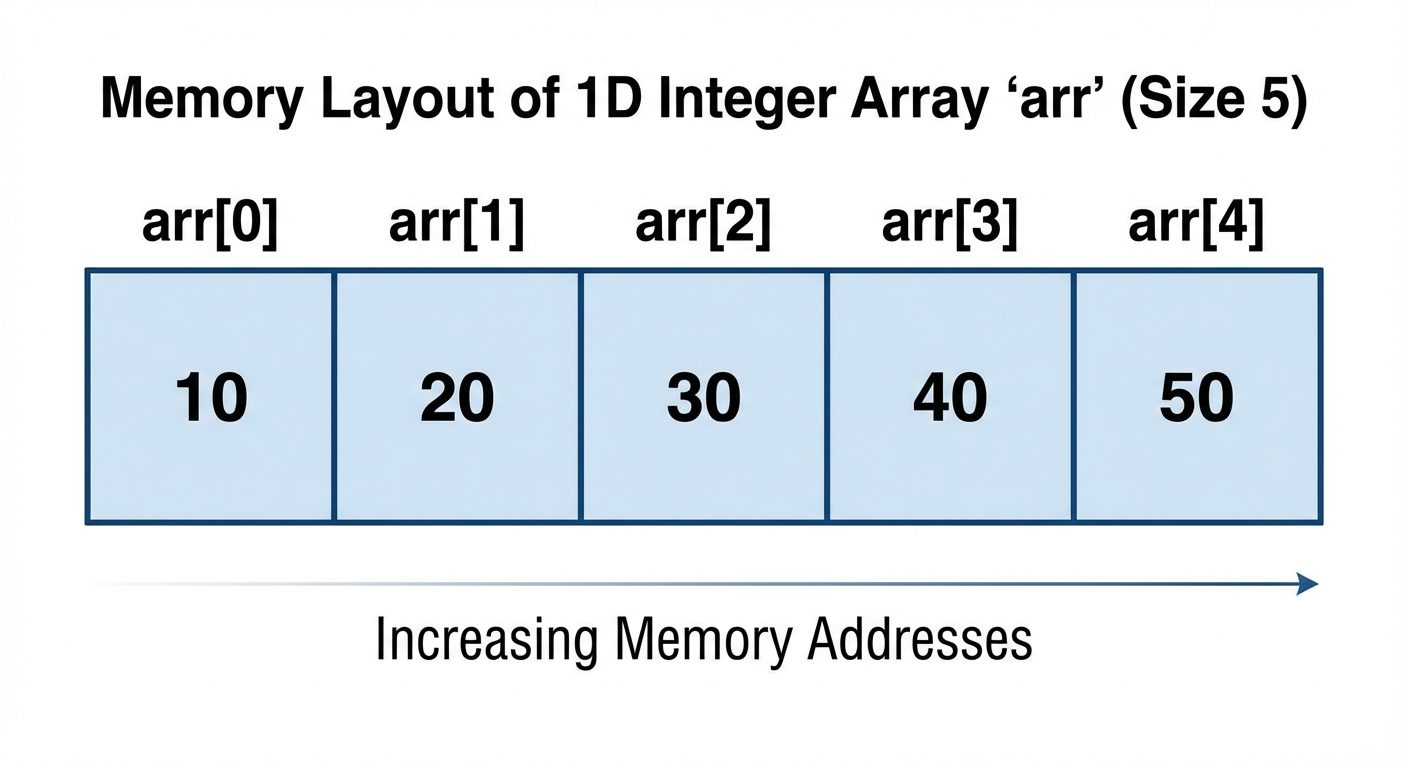
2. Declaring and Initializing Arrays

1-Dimensional Arrays

Declaration Syntax:

data_type array_name[array_size];

Initialization Methods:

1. Compile-time Initialization:
   

   C

       int numbers[5] = {10, 20, 30, 40, 50};
       int autoSize[] = {1, 2, 3}; // Size automatically determined as 3
       int partial[5] = {1, 2};    // Remaining elements initialized to 0
       

2. Runtime Initialization (Input Loop):
   

   C

       int arr[10];
       for(int i = 0; i < 10; i++) {
           scanf("%d", &arr[i]);
       }
       

2-Dimensional Arrays (Matrices)

A 2D array is essentially an "array of arrays," organized in rows and columns.

Declaration Syntax:

data_type array_name[rows][columns];

Initialization:

// Valid initialization
int matrix[2][3] = {
    {1, 2, 3},  // Row 0
    {4, 5, 6}   // Row 1
};

Processing 2D Arrays:
Nested loops are required to traverse 2D arrays.

for(int i = 0; i < rows; i++) {       // Outer loop for rows
    for(int j = 0; j < cols; j++) {   // Inner loop for columns
        printf("%d ", matrix[i][j]);
    }
    printf("\n");
}

3. Passing Arrays to Functions

When an array is passed to a function, it decays into a pointer to its first element. Therefore, arrays are passed by reference, meaning changes made inside the function affect the original array.

Syntax

void processArray(int arr[], int size) {
    // Operations on arr
}

int main() {
    int data[5] = {1, 2, 3, 4, 5};
    processArray(data, 5); // Pass only the name
    return 0;
}

Note: You cannot return a full array from a function directly in C (though you can return a pointer).

4. Array Applications

Arrays are fundamental data structures used in:

• Matrix Operations: Mathematical addition, multiplication, and transposition.
• Sorting and Searching: Organizing data for efficient retrieval.
• Strings: In C, strings are arrays of characters ending with a null character (\0).
• Databases: Storing records (often using arrays of structures).
• Signal Processing: Storing digitized signal samples.

5. Operations: Insertion and Deletion

Since arrays have a fixed size, inserting or deleting elements requires shifting existing elements.

Insertion

To insert an element at index pos, all elements from pos to the end must shift one position to the right.

void insert(int arr[], int *n, int pos, int val) {
    // *n is current size
    for (int i = *n - 1; i >= pos; i--) {
        arr[i + 1] = arr[i]; // Shift right
    }
    arr[pos] = val;
    (*n)++; // Increase size count
}

Deletion

To delete an element at index pos, all elements from pos + 1 to the end must shift one position to the left.

void delete(int arr[], int *n, int pos) {
    for (int i = pos; i < *n - 1; i++) {
        arr[i] = arr[i + 1]; // Shift left
    }
    (*n)--; // Decrease size count
}

6. Searching Algorithms

Searching is the process of finding the location of a specific element (target) in the array.

Linear Search

• Method: Checks every element sequentially from the start.
• Prerequisite: None (array can be unsorted).
• Complexity:
• Best Case: Element is at the first index.

int linearSearch(int arr[], int n, int key) {
    for(int i = 0; i < n; i++) {
        if(arr[i] == key) return i; // Found
    }
    return -1; // Not found
}

Binary Search

• Method: Divide and conquer. Compares target with the middle element. If target < middle, search left half; otherwise search right half.
• Prerequisite: Array MUST be sorted.
• Complexity:

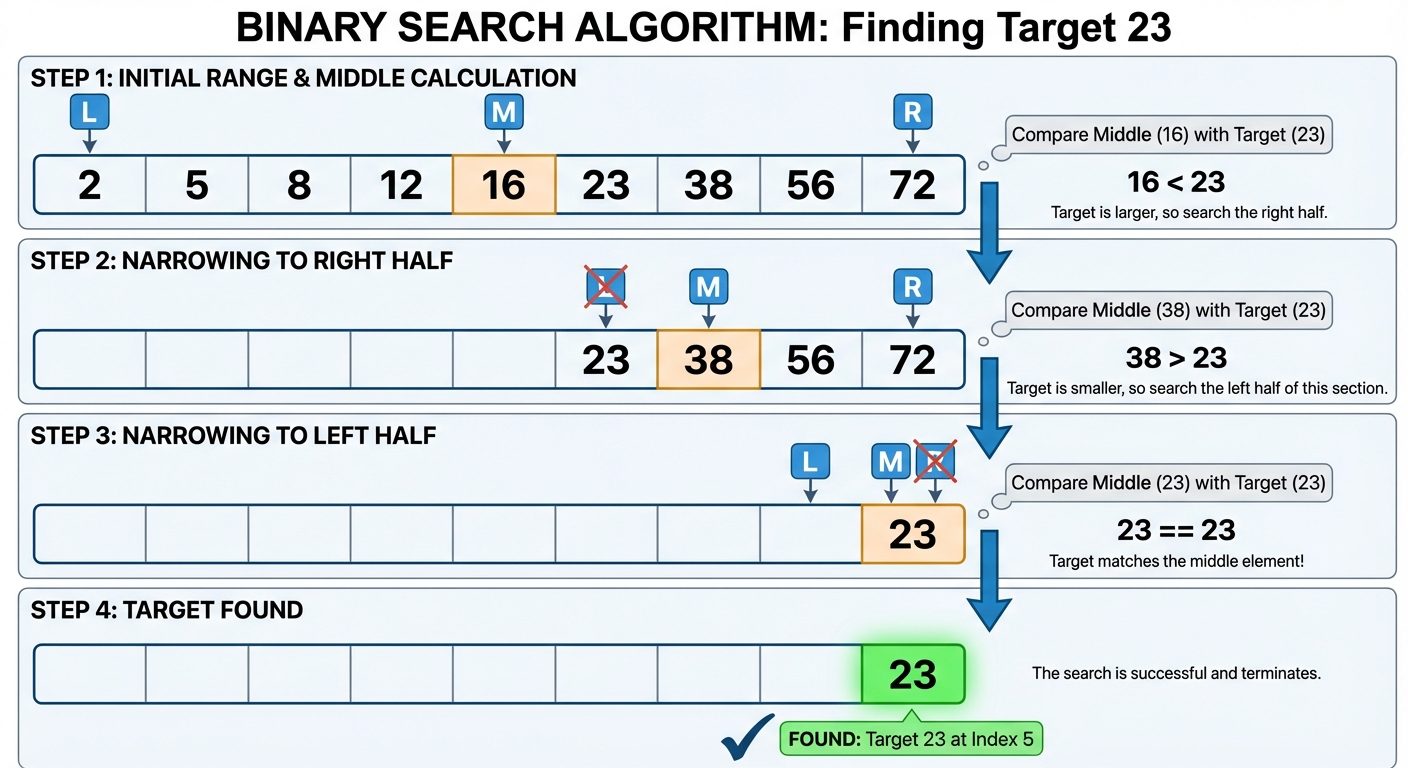
Binary Search Logic:

int binarySearch(int arr[], int n, int key) {
    int low = 0, high = n - 1;
    while (low <= high) {
        int mid = (low + high) / 2;
        if (arr[mid] == key)
            return mid;
        else if (arr[mid] < key)
            low = mid + 1;
        else
            high = mid - 1;
    }
    return -1;
}

7. Sorting: Bubble Sort

Sorting rearranges the array elements in ascending or descending order.

Bubble Sort Algorithm

Bubble Sort repeatedly steps through the list, compares adjacent elements, and swaps them if they are in the wrong order. The pass through the list is repeated until the list is sorted.

• Logic: After the first pass, the largest element "bubbles up" to the last position.
• Complexity:

![A diagram showing a single pass of the Bubble Sort algorithm on an array 5, 1, 4, 2, 8. The diagram should show sequential rows representing comparison steps. In the first row, show '5' and '1' highlighted with a curved arrow indicating a swap is needed. In the next row, show the result [1, 5, 4, 2, 8] with '5' and '4' highlighted for the next comparison. Continue this pattern until '8' reaches the end. Use color coding: yellow boxes for elements currently being compared, green boxes for elements that are sorted/locked at the end of the pass. Add text labels like "Compare", "Swap", and "Pass 1 Complete".]

Implementation:

void bubbleSort(int arr[], int n) {
    for (int i = 0; i < n - 1; i++) {       // Number of passes
        for (int j = 0; j < n - i - 1; j++) { // Comparison loop
            if (arr[j] > arr[j + 1]) {
                // Swap
                int temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
            }
        }
    }
}

Optimized Bubble Sort

If no swaps occur during a pass, the array is already sorted. A flag variable can be used to break the loop early, improving best-case performance to .